题目内容
16.解方程(1)$\frac{3}{x+1}=\frac{5}{x+3}$
(2)$\frac{1}{x+3}-\frac{1}{x-3}=\frac{2x}{{{x^2}-9}}$.
分析 (1)先把方程两边乘以(x+1)(x+3)得到整式方程,然后解整式方程,再进行检验确定原方程的解;
(2)先把方程两边乘以(x-3)(x+3)得到整式方程,然后解整式方程,再进行检验确定原方程的解.
解答 解:(1)去分母得到3(x+3)=5(x+1),
解得x=2,
检验:当x=2时,(x+1)(x+3)≠0,则x=2是原方程的解,
所以原方程的解为x=2;
(2)去分母得x-3-(x+3)=2x,
解得x=-3,
检验:当x=-3时,(x+3)(x-3)=0,则x=-3是原方程的增根,
所以原方程无解.
点评 本题考查了解分式方程:掌握解分式方程的步骤(去分母;求出整式方程的解;检验;得出结论).

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
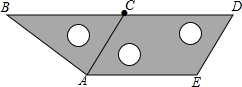 如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )
如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线段AB,BD,DE,EC,CA,AE中,相互平行的线段有( )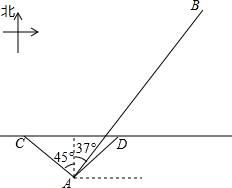 我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.
我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截. 如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.
如图,AB是半圆的直径,点C、D是半圆上两点,∠ADC=128°,则∠ABC=52°.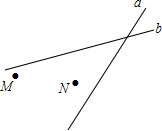 如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.
如图:某地有两所大学M、N和两条相交叉的公路a、b,现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案.