题目内容
14．已知关于x的一元二次方程kx2-（k-1）x+$\frac{1}{4}$k=0．（1）若方程有两个不相等的实数根，求k的取值范围；
（2）在（1）的条件下，当k取最大整数时，求该一元二次方程的解．
分析 （1）根据二次项系数非负结合根的判别式△＞0，即可得出关于k的一元一次不等式组，解之即可得出k的取值范围；
（2）由（1）的结论可找出k值，将其代入原方程中利用公式法解一元二次方程，即可得出结论．
解答 解：（1）∵关于x的一元二次方程kx2-（k-1）x+$\frac{1}{4}$k=0有两个不相等的实数根，
∴$\left\{\begin{array}{l}{k≠0}\\{△=[-（k-1）]^{2}-4k•\frac{1}{4}k＞0}\end{array}\right.$，
解得：k＜$\frac{1}{2}$且k≠0．
（2）∵k＜$\frac{1}{2}$且k≠0，
∴k取最大整数时k=-1，此时原方程为x2-2x+$\frac{1}{4}$=0，
解得：x1=1+$\frac{\sqrt{3}}{2}$，x2=1-$\frac{\sqrt{3}}{2}$．
点评 本题考查了根的判别式、一元二次方程的定义以及公式法解一元二次方程，解题的关键是：（1）根据二次项系数非负结合根的判别式△＞0，列出关于k的一元一次不等式组；（2）熟练掌握公式法解一元二次方程的应用．
练习册系列答案
相关题目
5．
阅读下列材料：
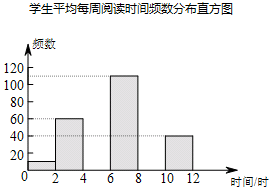
为引导学生广泛阅读古今文学名著，某校开展了读书月活动．学生会随机调查了部分学生平均每周阅读时间的情况，整理并绘制了如图的统计图表：
学生平均每周阅读时间频数分布表
请根据以上信息，解答下列问题：
（1）在频数分布表中，a=80，b=0.275；
（2）补全频数分布直方图；
（3）如果该校有1 600名学生，请你估计该校平均每周阅读时间不少于6小时的学生大约有1000人．
阅读下列材料：为引导学生广泛阅读古今文学名著，某校开展了读书月活动．学生会随机调查了部分学生平均每周阅读时间的情况，整理并绘制了如图的统计图表：
学生平均每周阅读时间频数分布表
| 平均每周阅读时间x（时） | 频数 | 频率 |
| 0≤x＜2 | 10 | 0.025 |
| 2≤x＜4 | 60 | 0.150 |
| 4≤x＜6 | a | 0.200 |
| 6≤x＜8 | 110 | b |
| 8≤x＜10 | 100 | 0.250 |
| 10≤x＜12 | 40 | 0.100 |
| 合计 | 400 | 1.000 |
（1）在频数分布表中，a=80，b=0.275；
（2）补全频数分布直方图；
（3）如果该校有1 600名学生，请你估计该校平均每周阅读时间不少于6小时的学生大约有1000人．
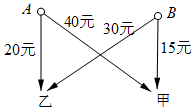我县黄泛区农场有A、B两个果园，分别收获水果380件，320件，现需把这些水果全部运往甲、乙两个销售点，每件运费如图所示．现甲销售点需水果400件，乙销售点需水果300件．
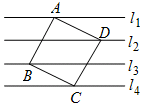如图，已知直线l1∥l2∥l3∥l4，且相邻两条平行直线间的距离都是d，如果正方形ABCD的四个顶点分别在四条直线上，且面积都是1，则d=$\frac{\sqrt{5}}{5}$．
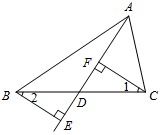完成下面的证明：