Question

2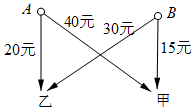．我县黄泛区农场有A、B两个果园，分别收获水果380件，320件，现需把这些水果全部运往甲、乙两个销售点，每件运费如图所示．现甲销售点需水果400件，乙销售点需水果300件．
（1）设从A果园运往甲销售点水果x件，总运费w元，请用含x的代数式表示w，并写出x 的取值范围．
（2）若总运费不超过18300元，且A地运往甲销售点的水果不低于200件，试确定运费最低的运输方案，并求最低运费．

Answer 1

分析 （1）根据题意可以用含x的代数式表示w，并写出x 的取值范围；
（2）根据（1）中的答案和一次函数及不等式的性质可以解答本题．

解答 解：（1）设A果园送往甲销售点x件，则由A果园送往乙销售点（380-x）件，由B果园送往甲销售点（400-x）件，由B果园送往乙销售点320-（400-x）=（x-80）件，w=40x+20（380-x）+15（400-x）+30（x-80）=35x+11200，
由$\left\{\begin{array}{l}380-x≥0\\ 400-x＞0\\ x-80≥0.\end{array}\right.$，得80≤x≤380，
即w=35x+11200（80≤x≤380）；
（2）由（1）可知w=35x+11200，
∵200≤x≤380，
∴当x=200时，w最小，此时，w=18200＜18300，
答：运费最低的方案是：A果园送往甲销售点200件，运往乙180件，B果园送往甲销售点200件，运往乙120件，最低费用是18200元．

点评 本题考查一次函数的应用、一元一次不等式组的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用一次函数的性质和不等式的性质解答．