题目内容
9.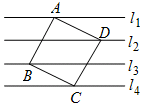 如图,已知直线l1∥l2∥l3∥l4,且相邻两条平行直线间的距离都是d,如果正方形ABCD的四个顶点分别在四条直线上,且面积都是1,则d=$\frac{\sqrt{5}}{5}$.
如图,已知直线l1∥l2∥l3∥l4,且相邻两条平行直线间的距离都是d,如果正方形ABCD的四个顶点分别在四条直线上,且面积都是1,则d=$\frac{\sqrt{5}}{5}$.
分析 过D点作直线EF与平行线垂直,与l1交于点E,与l4交于点F.易证△ADE≌△DFC,可得CF=DE=d,DF=2d,在Rt△CDF中,构建方程即可解决问题.
解答 解:作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠AED=∠DFC=90°.
∵四边形ABCD为正方形,
∴∠ADC=90°.
∴∠ADE+∠CDF=90°.
又∵∠ADE+∠DAE=90°,
∴∠CDF=∠DAE.
∵AD=CD,
∴△ADE≌△DCF,
∴CF=DE=d.
∵DF=2d,
在Rt△DCF中,∵CD2=CF2+DF2,
∴1=d2+4d2,
∴d=$\frac{\sqrt{5}}{5}$.
故答案为$\frac{\sqrt{5}}{5}$.
点评 题考查正方形的性质和面积计算,根据平行线之间的距离构造全等的直角三角形是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
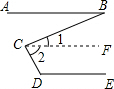 完成下面的证明:
完成下面的证明: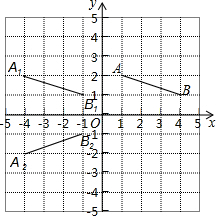 如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1),
如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(1,2)、(4,1),