Question

△ABC中，∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E，
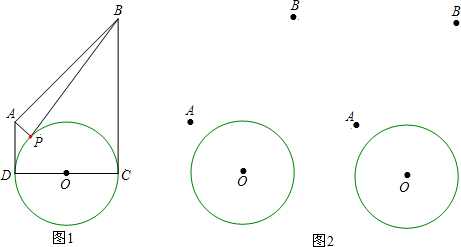
（1）如图1，若∠A=70°，求∠E的度数；
（2）如图2，若∠A=90°，则∠E=

 

；如图3，若∠A=130°，求∠E=

 

；
（3）根据上述结果，你发现∠A与∠E的关系是：

 

；并证明你的结论．

Answer 1

考点：三角形内角和定理,三角形的外角性质

专题：

分析：根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC，∠ECD=∠E+∠EBC，再根据角平分线的定义可得∠EBC=

1

2

∠ABC，∠ECD=

1

2

∠ACD，然后整理得到∠E=

1

2

∠A，再分别代入数据进行计算即可得解．

解答：解：由三角形的外角性质得，∠ACD=∠A+∠ABC，∠ECD=∠E+∠EBC，
∵∠ABC的平分线与∠ACB的外角∠ACM的平分线交于点E，
∴∠EBC=

1

2

∠ABC，∠ECD=

1

2

∠ACD，
∴∠E+∠EBC=

1

2

（∠A+∠ABC），
∴∠E=

1

2

∠A，
（1）∠A=70°时，∠E=

1

2

×70°=35°；
（2）∠A=90°时，∠E=

1

2

×90°=45°，
∠A=130°时，∠E=

1

2

×130°=65°；
（3）∠E=

1

2

∠A．
故答案为：（2）45°，65°；（3）∠E=

1

2

∠A．

点评：本题考查了三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义，熟记性质并整体思想的利用是解题的关键．