题目内容
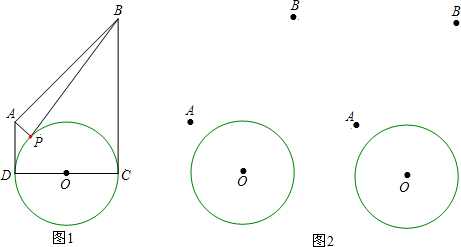
如图1,⊙O的直径CD=4,AD⊥DC,BC⊥DC,AD=2,BC=6,P是⊙O上的一个动点.
(1)记△APB的面积为S,求S的取值范围;
(2)在图2中,∠APB的大小是不断变化的,用语言描述当∠APB最大和最小时P点的位置(也可以附带作出大致的图形,在图形上标出P点的大致位置,不必说明理由).
(1)记△APB的面积为S,求S的取值范围;
(2)在图2中,∠APB的大小是不断变化的,用语言描述当∠APB最大和最小时P点的位置(也可以附带作出大致的图形,在图形上标出P点的大致位置,不必说明理由).

考点:圆的综合题
专题:综合题
分析:(1)连接AO交⊙O于P1,P2,作AE⊥BC于E,如图1,由OD=AD=2,AD⊥DC可判断△OAD为等腰直角三角形,根据等腰直角三角形的性质得OA=2
,∠OAD=45°,再证明四边形ADCE为矩形,得到AE=CD=4,CE=AD=2,则BE=BC-CE=4,又可判断△ABE为等腰直角三角形,所以AB=
BE=4
,∠BAE=45°,由于∠DAE=90°,则∠OAE=45°,于是得到∠OAB=∠BAE+∠OAE=90°,即OA⊥AB,根据与圆有关的性质得到P1点到AB的距离最小,则根据三角形面积公式得到S最小,可计算S的最小值为8-4
;P2点到AB的距离最大,S最大,可计算S的最大值为8+4
;∴S的取值范围为8-4
≤S≤8+4
;
(2)过A、B两点⊙M与⊙O外切于P点时,∠APB最大,因为除切点外,∠APB为⊙M的圆外角;过A、B两点的⊙N与⊙O内切于P点时,∠APB最小,因为除切点外,∠APB为⊙N的圆内角.
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
(2)过A、B两点⊙M与⊙O外切于P点时,∠APB最大,因为除切点外,∠APB为⊙M的圆外角;过A、B两点的⊙N与⊙O内切于P点时,∠APB最小,因为除切点外,∠APB为⊙N的圆内角.
解答: 解:(1)连接AO交⊙O于P1,P2,作AE⊥BC于E,如图1,
解:(1)连接AO交⊙O于P1,P2,作AE⊥BC于E,如图1,
∵OD=AD=2,AD⊥DC,
∴△OAD为等腰直角三角形,
∴OA=
OD=2
,∠OAD=45°,
∵BC⊥CD,AE⊥BC,
∴四边形ADCE为矩形,
∴AE=CD=4,CE=AD=2,BE=BC-CE=6-2=4,
∴△ABE为等腰直角三角形,
∴AB=
BE=4
,∠BAE=45°,
而∠DAE=90°,
 ∴∠OAE=45°,
∴∠OAE=45°,
∴∠OAB=∠BAE+∠OAE=90°,
∴OA⊥AB,
∴P1点到AB的距离最小,S最小,AP1=OA-OP1=2
-2,则S的最小值=
×4
×(2
-2)=8-4
;
P2点到AB的距离最大,S最大,AP2=OA+OP2=2
+2,则S的最大值=
×4
×(2
+2)=8+4
;
∴S的取值范围为8-4
≤S≤8+4
;
(2)过A、B两点⊙M与⊙O外切于P点时,∠APB最大;过A、B两点的⊙N与⊙O内切于P点时,∠APB最小,如图2.
 解:(1)连接AO交⊙O于P1,P2,作AE⊥BC于E,如图1,
解:(1)连接AO交⊙O于P1,P2,作AE⊥BC于E,如图1,∵OD=AD=2,AD⊥DC,
∴△OAD为等腰直角三角形,
∴OA=
| 2 |
| 2 |
∵BC⊥CD,AE⊥BC,
∴四边形ADCE为矩形,
∴AE=CD=4,CE=AD=2,BE=BC-CE=6-2=4,
∴△ABE为等腰直角三角形,
∴AB=
| 2 |
| 2 |
而∠DAE=90°,
 ∴∠OAE=45°,
∴∠OAE=45°,∴∠OAB=∠BAE+∠OAE=90°,
∴OA⊥AB,
∴P1点到AB的距离最小,S最小,AP1=OA-OP1=2
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
P2点到AB的距离最大,S最大,AP2=OA+OP2=2
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
∴S的取值范围为8-4
| 2 |
| 2 |
(2)过A、B两点⊙M与⊙O外切于P点时,∠APB最大;过A、B两点的⊙N与⊙O内切于P点时,∠APB最小,如图2.
点评:本题考查了圆的综合题:熟练掌握与圆有关的性质、圆周角定理和等腰直角三角形的判定与性质.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
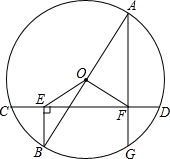 已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证:
已知,AB为圆O的直径,CD是弦,BE⊥CD于E,AF⊥CD于F,连接OE,OF,求证: 如图,在△ABC中,点D、E分别为BC、AD的中点,若S△ABC=1,求S△ABE.
如图,在△ABC中,点D、E分别为BC、AD的中点,若S△ABC=1,求S△ABE.