题目内容
已知x,y互为相反数,m,n互为倒数,a的绝对值是9,求2(x+y)-m•n+a的值.
考点:代数式求值,相反数,绝对值,倒数
专题:
分析:根据互为相反数的两个数的和等于0可得x+y=0,互为倒数的两个数的乘积是1可得mn=1,绝对值的性质求出a,然后代入代数式进行计算即可得解.
解答:解:∵x,y互为相反数,
∴x+y=0,
∵m,n互为倒数,
∴mn=1,
∵a的绝对值是9,
∴a=±9,
当a=9时,2(x+y)-m•n+a=2×0-1+9=8,
当a=-9时,2(x+y)-m•n+a=2×0-1-9=-10,
综上所述,代数式的值为8或-10.
∴x+y=0,
∵m,n互为倒数,
∴mn=1,
∵a的绝对值是9,
∴a=±9,
当a=9时,2(x+y)-m•n+a=2×0-1+9=8,
当a=-9时,2(x+y)-m•n+a=2×0-1-9=-10,
综上所述,代数式的值为8或-10.
点评:本题考查了代数式求值,主要利用了相反数的定义,倒数的定义和绝对值的性质,熟记概念与性质是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

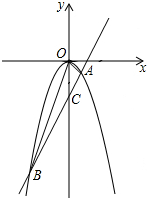 已知函数y=ax2(a≠0)与直线y=2x-3交于A(1,b)和点B,求S△ABO.
已知函数y=ax2(a≠0)与直线y=2x-3交于A(1,b)和点B,求S△ABO.