题目内容
把19,20,21…79,80写成连数A=192021…7980.证明:A|1980.
考点:数的整除性
专题:证明题
分析:先把1980分解为4×5×9×11,根据这个数A的末位数字为80,可以整除4和5,然后证明这个数A可以被9和11整除,即可证得A是1980的倍数.
解答:解:1980=4×5×9×11,
∵连数A=192021…7980,末位数字为80可以被4和5整除,
∴192021…7980可以被4和5整除,
∵数字192021…7980所有奇数位之和为:1+(2+3+4+5+6+7)×10+8=279,
数字192021…7980所有偶数位之和为:9+(0+1+2+3+4+5+6+7+8+9)×6+0=279,
奇数位数字之和=偶数位数字之和,
∴这个数可以被11整除,
又∵这个数所有数字之和=279+279=588可以被9整除,
∴这个数可以被9整除,
综上所述,A=192021…7980可以同时被4,5,9,11整除,
∴A是1980的倍数.
∵连数A=192021…7980,末位数字为80可以被4和5整除,
∴192021…7980可以被4和5整除,
∵数字192021…7980所有奇数位之和为:1+(2+3+4+5+6+7)×10+8=279,
数字192021…7980所有偶数位之和为:9+(0+1+2+3+4+5+6+7+8+9)×6+0=279,
奇数位数字之和=偶数位数字之和,
∴这个数可以被11整除,
又∵这个数所有数字之和=279+279=588可以被9整除,
∴这个数可以被9整除,
综上所述,A=192021…7980可以同时被4,5,9,11整除,
∴A是1980的倍数.
点评:本题考查了数的整除性,解答本题的关键先把数1980分解为4×5×9×11,分别证明数字192021…7980可以被4,5,9,11整除,难度较大.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目

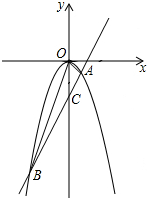 已知函数y=ax2(a≠0)与直线y=2x-3交于A(1,b)和点B,求S△ABO.
已知函数y=ax2(a≠0)与直线y=2x-3交于A(1,b)和点B,求S△ABO.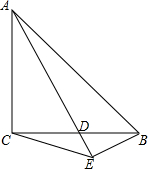 如图,在等腰Rt△ABC中,∠C=90°,点D是BC上任意一点,连接AD,过点B作BE垂直于AD,交射线AD于点E,连接CE,求∠AEC的度数.
如图,在等腰Rt△ABC中,∠C=90°,点D是BC上任意一点,连接AD,过点B作BE垂直于AD,交射线AD于点E,连接CE,求∠AEC的度数.