题目内容
15.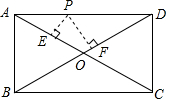 如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )
如图,P是矩形ABCD的边AD上一个动点,PE⊥AC于E,PF⊥BD于F,当P从A向D运动(P与A,D不重合),则PE+PF的值( )| A. | 增大 | B. | 减小 | C. | 不变 | D. | 先增大再减小 |
分析 首先过A作AG⊥BD于G.利用面积法证明PE+PF=AG即可.
解答 解:如图,过A作AG⊥BD于G,
则S△AOD=$\frac{1}{2}$×OD×AG,S△AOP+S△POD=$\frac{1}{2}$×AO×PF+$\frac{1}{2}$×DO×PE=$\frac{1}{2}$×DO×(PE+PF),
∵S△AOD=S△AOP+S△POD,四边形ABCD是矩形,
∴OA=OD,
∴PE+PF=AG,
∴PE+PF的值是定值,
故选C.
点评 本题考查矩形的性质、等腰三角形的性质、三角形的面积计算.解决本题的关键是证明等腰三角形底边上的任意一点到两腰距离的和等于腰上的高.

练习册系列答案
相关题目
5.$\sqrt{10}$是无理数,设它的整数部分为a,小数部分为b,则a-b的值为( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
6.下列计算正确的是( )
| A. | xy•xy=2xy | B. | 3$\sqrt{x}$-$\sqrt{x}$=3(x≥0) | C. | (2x)3=2x3 | D. | $\sqrt{x}$•$\sqrt{y}$=$\sqrt{xy}$(x≥0,y≥0) |
3.下列多项式中,在实数范围内能进行因式分解的是( )
| A. | a-1 | B. | a2-1 | C. | x2-4y | D. | a2+1 |
10.下列计算中,正确的是( )
| A. | x2+x4=x6 | B. | 2x+3y=5xy | C. | (x3)2=x6 | D. | x6÷x3=x2 |
20.某校九年级(1)班全体学生2017年初中毕业体育考试的成绩统计如表:
根据表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 25 | 29 | 26 | 24 | 27 | 28 | 30 |
| 人数(人) | 6 | 6 | 9 | 8 | 10 | 5 | 6 |
| A. | 该班一共有50名同学 | |
| B. | 该班学生这次考试成绩的众数是30分 | |
| C. | 该班学生这次考试成绩的中位数是27分 | |
| D. | 该班学生这次考试成绩的平均数是26.8分 |
5. 如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )
 如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )
如图,已知AB是⊙O的直径,∠D=36°,则∠CAB的度数为( )| A. | 18° | B. | 36° | C. | 54° | D. | 72° |




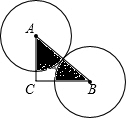 如图,Rt△ABC中,∠C=90°,AC=4,BC=4$\sqrt{3}$,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=4$\sqrt{3}$,两等圆⊙A,⊙B外切,那么图中两个扇形(即阴影部分)的面积之和为( )