题目内容
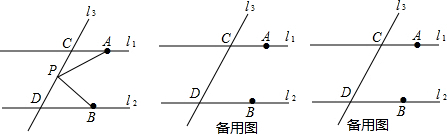
已知直线L1∥L2,直线L3与直线L1、L2交与C、D两点,点A、B分别是直线L1和L2上,且在直线L3上同一侧,点P是L1上一动点,不与两点C、D重合.
(1)如果点P在线段C、D两点之间运动时(图1),连接AP、BP,那么∠PAC、∠PBD、∠APB之间具有怎样的数量关系的关系?请说明理由.
(2)如果点P在C、D两点的外侧运动时(备用图),连接AP、BP,那么∠PAC、∠PBD、∠APB之间具有怎样的数量关系的关系?请说明理由.
(1)如果点P在线段C、D两点之间运动时(图1),连接AP、BP,那么∠PAC、∠PBD、∠APB之间具有怎样的数量关系的关系?请说明理由.
(2)如果点P在C、D两点的外侧运动时(备用图),连接AP、BP,那么∠PAC、∠PBD、∠APB之间具有怎样的数量关系的关系?请说明理由.

考点:平行线的性质
专题:
分析:(1)过P点做PM∥L1,根据两直线平行,内错角相等即可证得;
(2)当点P在C点外侧运动时,过P点做PM∥L1,根据两直线平行,内错角相等即可证得;当点P在D点外侧运动时,同(2)可证得.
(2)当点P在C点外侧运动时,过P点做PM∥L1,根据两直线平行,内错角相等即可证得;当点P在D点外侧运动时,同(2)可证得.
解答: (1)解:如图1可知∠APB=∠PAC+∠PBD.
(1)解:如图1可知∠APB=∠PAC+∠PBD.
证明:过P点做PM∥L1.
∵L1∥L2,
∴PM∥L1∥L2,
∴∠APM=∠PAC,∠MPB=∠PBD,
∴∠APM+∠MPB=∠PAC+∠PBD.
∵∠APM+∠MPB=∠APB,
∴∠APB=∠PAC+∠PBD;
(2)解:当点P在C点外侧运动时,(备用图1)
可得∠APB=∠PBD-∠PAC.
证明:过P点做PM∥L1.
∵L1∥L2,
∴PM∥L1∥L2,
∴∠APM=∠PAC,∠MPB=∠PBD,
∴∠MPB-∠MPA=∠PBD-∠PAC,
∵∠MPB-∠MPA=∠APB,
∴∠APB=∠PBD-∠PAC;
当点P在D点外侧运动时,(备用图2)
可得∠APB=∠PAC-∠PBD.
证明:过P点做PM∥L1,
∵L1∥L2,
∴PM∥L1∥L2
∴∠APM=∠PAC,∠MPB=∠PBD,
∴∠MPA-∠MPB=∠PAC-∠PBD,
∵∠MPA-∠MPB=∠APB,
∴∠APB=∠PAC-∠PBD.
 (1)解:如图1可知∠APB=∠PAC+∠PBD.
(1)解:如图1可知∠APB=∠PAC+∠PBD.证明:过P点做PM∥L1.
∵L1∥L2,
∴PM∥L1∥L2,
∴∠APM=∠PAC,∠MPB=∠PBD,
∴∠APM+∠MPB=∠PAC+∠PBD.
∵∠APM+∠MPB=∠APB,
∴∠APB=∠PAC+∠PBD;
(2)解:当点P在C点外侧运动时,(备用图1)
可得∠APB=∠PBD-∠PAC.
证明:过P点做PM∥L1.
∵L1∥L2,
∴PM∥L1∥L2,
∴∠APM=∠PAC,∠MPB=∠PBD,
∴∠MPB-∠MPA=∠PBD-∠PAC,
∵∠MPB-∠MPA=∠APB,
∴∠APB=∠PBD-∠PAC;
当点P在D点外侧运动时,(备用图2)
可得∠APB=∠PAC-∠PBD.
证明:过P点做PM∥L1,
∵L1∥L2,
∴PM∥L1∥L2
∴∠APM=∠PAC,∠MPB=∠PBD,
∴∠MPA-∠MPB=∠PAC-∠PBD,
∵∠MPA-∠MPB=∠APB,
∴∠APB=∠PAC-∠PBD.
点评:本题利用了平行线的性质:两直线平行,内错角相等,正确作出辅助线,以及注意(3)中分情况讨论是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列事件:?①浦东明天是晴天,②?铅球浮在水面上,?③平面中,多边形的外角和都等于360度,属于确定事件的个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,将一张矩形纸片对折后再对折,然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )
如图,将一张矩形纸片对折后再对折,然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是( )| A、矩形 | B、平行四边形 |
| C、梯形 | D、菱形 |
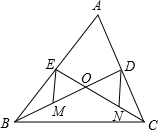 如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.
如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F.