题目内容
已知等腰△ABC中，AB=AC，一腰上的中线BD把这个△ABC的周长分成15cm和6cm两部分，求这个等腰三角形的各边长？（提示：用方程思想解决）考点：等腰三角形的性质
专题：
分析：设AB=AC=2x，BC=y，则AD=CD=x，则有两种情况，根据等腰三角形的性质以及三角形三边关系解答．
解答：解：设AB=AC=2x，BC=y，则AD=CD=x，
∵AC上的中线BD将这个三角形的周长分成15和6两部分，
∴有两种情况：
①当3x=15，且x+y=6，
解得x=5，y=1，
∴三边长分别为10，10，1；
②当x+y=15且3x=6时，
解得X=2，y=13，此时腰为4，
根据三角形三边关系，任意两边之和大于第三边，而4+4=8＜13，
故这种情况不存在．
∴这个等腰三角形的各边长分别为10，10，1．
∵AC上的中线BD将这个三角形的周长分成15和6两部分，
∴有两种情况：
①当3x=15，且x+y=6，
解得x=5，y=1，
∴三边长分别为10，10，1；
②当x+y=15且3x=6时，
解得X=2，y=13，此时腰为4，
根据三角形三边关系，任意两边之和大于第三边，而4+4=8＜13，
故这种情况不存在．
∴这个等腰三角形的各边长分别为10，10，1．
点评：本题考查了等腰三角形和三角形三边关系求解，注意要分两种情况讨论是正确解答本题的关键．
练习册系列答案
相关题目
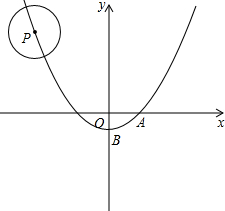如图，⊙P的半径为r，圆心P在抛物线y=ax2+c上运动．抛物线与x轴和y轴分别交与点A（1，0）点B（0，-1）．
正方形和圆都是人们比较喜欢的图形，给人以美得感受．我校数学兴趣小组在研究性学习中发现：
一个动点A在平面直角坐标系中作折线运动，第一次从点（-1，1）到A1（0，1），第二次运动到A2（3，-1），第三次运动到A3（8，1），第四次运动到A4（15，-1）…，按这样的运动规律，经过第13次运动后，动点A10的坐标是