题目内容
阅读下列材料:
问题:如图1,在?ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG=AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理使问题得到解决.参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

问题:如图1,在?ABCD中,E是AD上一点,AE=AB,∠EAB=60°,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
求证:EG=AG+BG.
小明同学的思路是:作∠GAH=∠EAB交GE于点H,构造全等三角形,经过推理使问题得到解决.参考小明同学的思路,探究并解决下列问题:
(1)完成上面问题中的证明;
(2)如果将原问题中的“∠EAB=60°”改为“∠EAB=90°”,原问题中的其它条件不变(如图2),请探究线段EG、AG、BG之间的数量关系,并证明你的结论.

考点:四边形综合题
专题:
分析:(1)作∠GAH=∠EAB交GE于点H,则∠GAB=∠HAE,先根据ASA定理得出△ABG≌△AEH,由∠GAH=∠EAB=60°可知△AGH是等边三角形,故可得出结论;
(2)作∠GAH=∠EAB交GE的延长线于点H,先根据ASA定理得出△ABG≌△AEH,故可得出BG=EH,AG=AH,根据∠GAH=∠EAB=90°可知△AGH是等腰直角三角形,所以
AG=HG,由此可得出结论.
(2)作∠GAH=∠EAB交GE的延长线于点H,先根据ASA定理得出△ABG≌△AEH,故可得出BG=EH,AG=AH,根据∠GAH=∠EAB=90°可知△AGH是等腰直角三角形,所以
| 2 |
解答: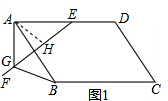 解:(1)证明:如图1,作∠GAH=∠EAB交GE于点H,则∠GAB=∠HAE.
解:(1)证明:如图1,作∠GAH=∠EAB交GE于点H,则∠GAB=∠HAE.
∵∠EAB=∠EGB,∠GAB=∠HAE,
∴∠ABG=∠AEH.
∵又∵AB=AE,
∴
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=60°,
∴△AGH是等边三角形.
∴AG=HG.
∴EG=AG+BG;
(2)线段EG、AG、BG之间的数量关系是EG=
AG-BG.
理由如下:
如图2,作∠GAH=∠EAB交GE的延长线于点H,则∠GAB=∠HAE.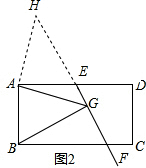
∵∠EGB=∠EAB=90°,
∴∠ABG+∠AEG=∠AEG+∠AEH=180°.
∴∠ABG=∠AEH.
又∵AB=AE,
∴
,
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=90°,
∴△AGH是等腰直角三角形.
∴
AG=HG,
∴EG=
AG-BG.
 解:(1)证明:如图1,作∠GAH=∠EAB交GE于点H,则∠GAB=∠HAE.
解:(1)证明:如图1,作∠GAH=∠EAB交GE于点H,则∠GAB=∠HAE.∵∠EAB=∠EGB,∠GAB=∠HAE,
∴∠ABG=∠AEH.
∵又∵AB=AE,
∴
|
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=60°,
∴△AGH是等边三角形.
∴AG=HG.
∴EG=AG+BG;
(2)线段EG、AG、BG之间的数量关系是EG=
| 2 |
理由如下:
如图2,作∠GAH=∠EAB交GE的延长线于点H,则∠GAB=∠HAE.

∵∠EGB=∠EAB=90°,
∴∠ABG+∠AEG=∠AEG+∠AEH=180°.
∴∠ABG=∠AEH.
又∵AB=AE,
∴
|
∴△ABG≌△AEH.
∴BG=EH,AG=AH.
∵∠GAH=∠EAB=90°,
∴△AGH是等腰直角三角形.
∴
| 2 |
∴EG=
| 2 |
点评:本题考查的是四边形综合题,涉及到全等三角形的判定与性质、直角三角形的性质、勾股定理等知识,难度适中.

练习册系列答案
相关题目


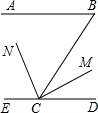 如图,已知AB∥CD,∠B=70°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
如图,已知AB∥CD,∠B=70°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.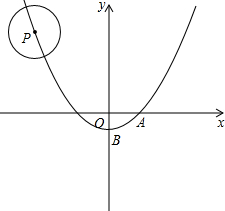 如图,⊙P的半径为r,圆心P在抛物线y=ax2+c上运动.抛物线与x轴和y轴分别交与点A(1,0)点B(0,-1).
如图,⊙P的半径为r,圆心P在抛物线y=ax2+c上运动.抛物线与x轴和y轴分别交与点A(1,0)点B(0,-1).