题目内容
6.求1+2+22+23…+22014的值,可令S=1+2+22+23…+22014,则2S=2+22+23+24+…+22015,因此2S-S=22015-1,
仿照以上推理,计算出1+5+52+53+…+52014的值为$\frac{{5}^{2015}-1}{4}$.
分析 令S=1+5+52+53+…+52014,则5S=5+52+53+…+52014+52015,二者做差后即可得出4S=52015-1,两边同时÷4即可得出结论.
解答 解:令S=1+5+52+53+…+52014,则5S=5+52+53+…+52014+52015,
∴5S-S=4S=52015-1,
∴S=$\frac{{5}^{2015}-1}{4}$.
故答案为:$\frac{{5}^{2015}-1}{4}$.
点评 本题考查了规律型中数字的变化类以及有理数的混合运算,仿照例题求出S的值是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
14.已知a、b为实数,则a2+ab+b2-a-2b的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
16.若反比例函数y=$\frac{k}{x}$(k≠0)经过(-2,3),则这个反比例函数一定经过( )
| A. | (-2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
 如图,在?ABCD中,BD是对角线,点M是BC的中点.若AD=10,BD=12,AM=9.则?ABCD面积是72.
如图,在?ABCD中,BD是对角线,点M是BC的中点.若AD=10,BD=12,AM=9.则?ABCD面积是72.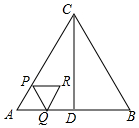 如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以1cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).
如图,△ABC是等边三角形,AB=4cm,CD⊥AB于点D,动点P从点A出发,沿AC以1cm/s的速度向终点C运动,当点P出发后,过点P作PQ∥BC交折线AD-DC于点Q,以PQ为边作等边三角形PQR,设四边形APRQ与△ACD重叠部分图形的面积为S(cm2),点P运动的时间为t(s).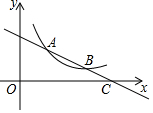 如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,与x轴交于点C(x0,0)
如图,已知直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)在第一象限内交于A(x1,y1),B(x2,y2)两点,与x轴交于点C(x0,0)