题目内容
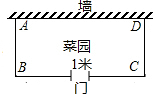如图，用长为39米的篱笆（虚线部分），一面靠墙围成矩形ABCD菜园（AB＜BC，且在边BC上开一个1米宽的门．（1）要使围成的矩形ABCD菜园面积为128米2，那么矩形一边AB长应为多少米？
（2）可围成的矩形ABCD菜园的最大面积为多少平方米？此时矩形一边AB长为多少米？
考点：二次函数的应用,一元二次方程的应用
专题：几何图形问题
分析：（1）根据题意表示出BC的长，进而利用矩形面积公式求出即可；
（2）利用矩形面积公式得出矩形面积与x的函数关系式进而求出最值．
（2）利用矩形面积公式得出矩形面积与x的函数关系式进而求出最值．
解答：（1）设矩形一边AB长为xm．则BC的长为（39-2x+1）m
根据题意，得x（39-2x+1）=128，即x2-20x+64=0，
解得：xl=4，x2=16．
因为AB＜BC，所以AB=4m．
故要使围成的菜园面积为128米2，矩形一边AB应为4米．
（2）设菜园的面积为Sm2，
则S=x（39-2x+1）=-2x2+40x=-2（x-10）2+200．
当x=10时，S取最大值，是200m2
故菜园的最大面积为200m2，此时AB为10m．
根据题意，得x（39-2x+1）=128，即x2-20x+64=0，
解得：xl=4，x2=16．
因为AB＜BC，所以AB=4m．
故要使围成的菜园面积为128米2，矩形一边AB应为4米．
（2）设菜园的面积为Sm2，
则S=x（39-2x+1）=-2x2+40x=-2（x-10）2+200．
当x=10时，S取最大值，是200m2
故菜园的最大面积为200m2，此时AB为10m．
点评：此题主要考查了二次函数的应用以及一元二次方程的应用，得出正确的等量关系是解题关键．
练习册系列答案
相关题目
如图：△ABC中，AB=AC=12，∠A=36°，AB的垂直平分线DE交AB、AC于D、E，
下例函数中是二次函数的有（ ）
①y=x+
；②y=3（x+1）2-1；③y=（x+3）2-2x2；④y=
+x．
①y=x+
| 1 |
| 2 |
| 1 |
| x2 |
| A、1个 | B、2个 | C、3个 | D、4个 |