题目内容
观察下面三行数:
-3,9,-27,81,-243,729…; ①
0,12,-24,84,-240,732…; ②
-1,3,-9,27,-81,243…. ③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第8个数,计算这3个数的和.
-3,9,-27,81,-243,729…; ①
0,12,-24,84,-240,732…; ②
-1,3,-9,27,-81,243…. ③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)取每行数的第8个数,计算这3个数的和.
考点:规律型:数字的变化类
专题:
分析:(1)观察可看出第一行的数分别是-3的1次方,二次方,三次方,四次方…且偶数项是正数,奇数项是负数,用式子表示规律为:(-3)n;
(2)观察②,③两行的数与第①行的联系,便不难求解;
(3)写出每一行的第8个数,然后相加即可得解.
(2)观察②,③两行的数与第①行的联系,便不难求解;
(3)写出每一行的第8个数,然后相加即可得解.
解答:解:(1)∵-3,9,-27,81,-243,729…;
∴第①行数是:(-3)1,(-3)2,(-3)3,(-3)4,
(2)第②行数比第①行数相应的数大3.即:(-3)1+3,(-3)2+3,(-3)3+3,(-3)4+3,…[答案形式不唯一],
第③行数的是第①行数数的
.
即:(-3)1×
,(-3)2×
,(-3)3×
,(-3)4×
,…[答案形式不唯一];
(3)第①行第8个数是:(-3)8,
第②行第8个数是:(-3)8+3,
第③行第8个数是:(-3)8×
.
所以这三个数的和是:
(-3)8+[(-3)8+3]+[(-3)8×
]
=6561+6564+2187
=15312.
∴第①行数是:(-3)1,(-3)2,(-3)3,(-3)4,
(2)第②行数比第①行数相应的数大3.即:(-3)1+3,(-3)2+3,(-3)3+3,(-3)4+3,…[答案形式不唯一],
第③行数的是第①行数数的
| 1 |
| 3 |
即:(-3)1×
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(3)第①行第8个数是:(-3)8,
第②行第8个数是:(-3)8+3,
第③行第8个数是:(-3)8×
| 1 |
| 3 |
所以这三个数的和是:
(-3)8+[(-3)8+3]+[(-3)8×
| 1 |
| 3 |
=6561+6564+2187
=15312.
点评:此题主要考查了数字变化规律,比较简单,观察得出每行之间的关系是解题的关键.

练习册系列答案
相关题目
在数轴上与-3距离2个单位长度的点表示的数是( )
| A、-1 | B、-5 |
| C、-1和-5 | D、1和-5 |
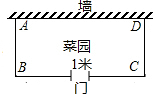 如图,用长为39米的篱笆(虚线部分),一面靠墙围成矩形ABCD菜园(AB<BC,且在边BC上开一个1米宽的门.
如图,用长为39米的篱笆(虚线部分),一面靠墙围成矩形ABCD菜园(AB<BC,且在边BC上开一个1米宽的门. 在边长为a的正方形ABCD内接一个正方形EFGH,设AE=x,正方形EFGH的面积为y.
在边长为a的正方形ABCD内接一个正方形EFGH,设AE=x,正方形EFGH的面积为y.