题目内容
19．
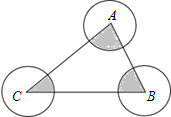如图，⊙A，⊙B，⊙C的半径都是2cm，则图中三个扇形（即阴影部分）面积之和是（ ）| A． | 2π | B． | π | C． | $\frac{1}{2}π$ | D． | 6π |
分析 根据三角形的内角和是180°和扇形的面积公式进行计算．
解答 解：∵∠A+∠B+∠C=180°，
∴阴影部分的面积=$\frac{180π×{2}^{2}}{360}$=2π．
故选A．
点评 考查了扇形面积的计算，因为三个扇形的半径相等，所以不需知道各个扇形的圆心角的度数，只需知道三个圆心角的和即可．
练习册系列答案
相关题目
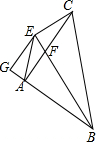如图，△ABC中，AB=AC，∠BAC=90°，BE平分∠ABC交AC于F，CE⊥BF于E，EG⊥AB于G，连AE．下列结论：①AB+AF=BC；②BF=2CE；③FC=GE；④∠GEA=∠CBF．其中正确的有（ ）
已知在△ABC中，∠BAC=90°，AD⊥BC于点D，点E为AC中点，延长ED、AB交于点F．求证：$\frac{AB}{AC}$=$\frac{DF}{FA}$．
如图数表是由从1 开始的连续自然数组成．下面所给的判断中，正确的有①②③．（填序号）