题目内容
9. 如图数表是由从1 开始的连续自然数组成.下面所给的判断中,正确的有①②③.(填序号)
如图数表是由从1 开始的连续自然数组成.下面所给的判断中,正确的有①②③.(填序号)①表中第8行的最后一个数是64;
②第n行的第一个数是(n-1)2+1;
③第n行的最后一个数是n2;
④第n行共有2n个数.
分析 观察每一行的最后一个数,可以发现第n行的最后一个数为n2,由此就可解决问题.
解答 解:第一行的最后一个数为1=12,
第二行的最后一个数为4=22,
第三行的最后一个数为9=32,
…
第(n-1)行的最后一个数为(n-1)2,
第n行的最后一个数为n2.
由此可得:
①表中第8行的最后一个数是82=64;
②第n行的第一个数是(n-1)2+1;
③第n行的最后一个数是n2;
④第n行共有[n2-(n-1)2]即(2n-1)个数.
故答案为①②③.
点评 本题属于规律探究题,发现第n行的最后一个数为n2,是解决本题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
19.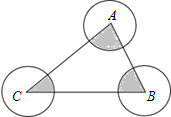 如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
 如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )| A. | 2π | B. | π | C. | $\frac{1}{2}π$ | D. | 6π |
4. 如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.
如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.
 如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.
如图,△ABC≌△DEF,∠F=58°,则∠C=( )度.| A. | 32° | B. | 58° | C. | 68° | D. | 44° |
18.函数y=2x+1与y=-$\frac{1}{2}$x+6的图象的交点坐标是( )
| A. | (-1,-1) | B. | (2,5) | C. | (1,6) | D. | (-2,5) |
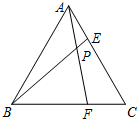 等边三角形ABC的边长为2$\sqrt{3}$,在AC,BC边上各有一个动点E,F,满足AE=CF,连接AF,BE相交于点P.
等边三角形ABC的边长为2$\sqrt{3}$,在AC,BC边上各有一个动点E,F,满足AE=CF,连接AF,BE相交于点P.