题目内容
7.函数y=-2x2+x图象的对称轴是$\frac{1}{4}$,最大值是$\frac{1}{8}$.分析 把抛物线解析式整理成顶点式形式,进一步解答即可.
解答 解:∵y=-2x2+x=-2(x-$\frac{1}{4}$)2+$\frac{1}{8}$,
∴对称轴是直线x=$\frac{1}{4}$,函数值的最大值是$\frac{1}{8}$.
故答案为:$\frac{1}{4}$,$\frac{1}{8}$.
点评 本题考查了二次函数的性质,把函数解析式整理成顶点式求对称轴和顶点坐标是解决问题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
2. 如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )
如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )
 如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )
如图,已知a∥b∥c,a,b间的距离为2,b,c间的距离为6,等腰直角三角尺的三个顶点A,B,C分别在a,b,c三条直线上,则边BC的长是( )| A. | 10 | B. | 8 | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{3}$ |
19.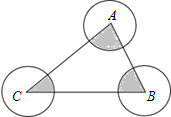 如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
 如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )
如图,⊙A,⊙B,⊙C的半径都是2cm,则图中三个扇形(即阴影部分)面积之和是( )| A. | 2π | B. | π | C. | $\frac{1}{2}π$ | D. | 6π |
 如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8.
如图,∠BAC=30°,点P是∠BAC平分线上一点,PM∥AC交AB于点M,PD⊥AC于点D,若PD+PM=12,则AM=8. 已知:AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:
已知:AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证: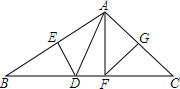 如图,在△ABC中,DE、FG分别为AB、AC的垂直平分线,连接AD、AF.
如图,在△ABC中,DE、FG分别为AB、AC的垂直平分线,连接AD、AF.