题目内容
2. 如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.(1)当BE平行CF时,证△BEH≌△CFH
(2)在问题(1)中,当BH与EH满足什么关系时,四边形BFCE是矩形,请说明理由.
分析 (1)由平行线的性质得出∠BEH=∠CFH时,由AAS证明△BEH≌△CFH即可;
(2)由全等三角形的性质得出BE=CF,EH=FH,得出四边形BFCE是平行四边形,再证出BC=EF,即可得出四边形BFCE是矩形.
解答 (1)证明:∵点H是BC的中点,
∴BH=CH,
∵BE∥CF,
∴∠BEH=∠CFH,
在△BEH和△CFH中,$\left\{\begin{array}{l}{∠BEH=∠CFH}&{\;}\\{∠CHE=∠CHF}&{\;}\\{BH=CH}&{\;}\end{array}\right.$,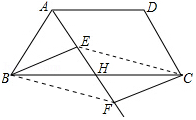
∴△BEH≌△CFH(HAS);
(2)解:当BH=EH时,四边形BFCE是矩形;理由如下:
连接BF、CE,如图所示:
∵△BEH≌△CFH,
∴BE=CF,EH=FH,
∵BE∥CF,
∴四边形BFCE是平行四边形,
又∵BH=CH,
∴BC=EF,
∴四边形BFCE是矩形(对角线相等的平行四边形为矩形).
点评 本题考查了全等三角形的判定和性质、平行线的性质、平行四边形的判定、矩形的判定,熟练掌握矩形的判定,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
12.关于x的方程ax2-2x+1=0有两个实数根,则a的取值范围是( )
| A. | .a≤1 | B. | .a<1 | C. | .a≤1且a≠0 | D. | a<1且a≠0 |
10. 如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;
②∠DMA=60°;
③△BPQ为等边三角形;
其中结论正确的有( )
 如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;
②∠DMA=60°;
③△BPQ为等边三角形;
其中结论正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个. |
7. 如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
 如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )| A. | 5 cm | B. | 6 cm | C. | 7 cm | D. | 8 cm |
14.下列各数中,无理数是( )
| A. | $\sqrt{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{22}{7}$ | D. | 0.16 |
11. 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 135° |