题目内容
 如图,直线y=-
如图,直线y=-| 1 |
| 4 |
| k |
| x |
| A、-2 | B、-4 | C、-6 | D、-8 |
考点:反比例函数与一次函数的交点问题
专题:
分析:首先过A作AD⊥BC于D,先求出直线=-
x-1与x轴交点B的坐标(-4,0),由过点B作x轴垂线交双曲线于点C,可求得点C的坐标,由AB=AC,根据三线合一的性质即可求得点D的坐标,继而求得点A的坐标,则可求得答案.
| 1 |
| 4 |
解答:解:过A作AD⊥BC于D,如图,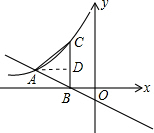
对于y=-
x-1,令y=0,则-
x-1=0,解得x=-4,
∴B点坐标为(-4,0),
∵CB⊥x轴,
∴C点的横坐标为-4,
对于y=
,
当x=-4,则y=-
,
∴C点坐标为(-4,-
),
∵AC=AB,AD⊥BC,
∴DC=DB,
∴D点坐标为(-4,-
),
∴A点的纵坐标为-
,
而点A在函数y=
的图象上,
把y=-
代入y=
得x=-8,
∴点A的坐标为(-8,-
),
把A(-8,-
)代入y=-
x-1得-
=-
×(-8)-1,
∴k=-8.
故选D.

对于y=-
| 1 |
| 4 |
| 1 |
| 4 |
∴B点坐标为(-4,0),
∵CB⊥x轴,
∴C点的横坐标为-4,
对于y=
| k |
| x |
当x=-4,则y=-
| k |
| 4 |
∴C点坐标为(-4,-
| k |
| 4 |
∵AC=AB,AD⊥BC,
∴DC=DB,
∴D点坐标为(-4,-
| k |
| 8 |
∴A点的纵坐标为-
| k |
| 8 |
而点A在函数y=
| k |
| x |
把y=-
| k |
| 8 |
| k |
| x |
∴点A的坐标为(-8,-
| k |
| 8 |
把A(-8,-
| k |
| 8 |
| 1 |
| 4 |
| k |
| 8 |
| 1 |
| 4 |
∴k=-8.
故选D.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两个函数的解析式.也考查了与x轴垂直的直线上所有点的横坐标相同以及等腰三角形的性质.

练习册系列答案
相关题目
 如图,一架长2.5m的梯子AB靠在一竖直的墙上,这时梯子的底端A到墙根O的距离为0.7m,如果梯子的顶端B下滑0.4m至B′,那么梯足将滑动( )
如图,一架长2.5m的梯子AB靠在一竖直的墙上,这时梯子的底端A到墙根O的距离为0.7m,如果梯子的顶端B下滑0.4m至B′,那么梯足将滑动( )| A、0.9m | B、1.5m |
| C、0.8m | D、0.5m |
如果把分式
中x和y的值都扩大为原来的n倍(n≠0且n≠1),那么这个分式的值( )
| 2x-y |
| x+2y |
| A、扩大n倍 | ||
B、缩小为原来的
| ||
| C、不变 | ||
| D、不能确定 |
下列代数式中,是最简分式的为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比.如图是将某年级60篇学生调查报告进行整理,分成5组画出的频数分布直方图.已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的调查报告有(分别大于或等于80分为优秀,且分数为整数)( )
某校在“创新素质实践行”活动中,组织学生进行社会调查,并对学生的调查报告进行了评比.如图是将某年级60篇学生调查报告进行整理,分成5组画出的频数分布直方图.已知从左到右5个小长方形的高的比为1:3:7:6:3,那么在这次评比中被评为优秀的调查报告有(分别大于或等于80分为优秀,且分数为整数)( )| A、18篇 | B、24篇 |
| C、25篇 | D、27篇 |
有长为2cm、3cm、4cm、5cm的四根木棒,选其中的3根作为三角形的边,可以围成的三角形的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |