��Ŀ����
15��̽�����⣺��1������������ͼ�٣���������ABCD�У���E��F�ֱ�ΪDC��BC���ϵĵ㣬�������EAF=45�㣬����EF����֤��DE+BF=EF��
������ⷽ���������������գ�
����ADE�Ƶ�A˳ʱ����ת90��õ���ABG����ʱAB��AD�غϣ�����ת�ɵã�
AB=AD��BG=DE����1=��2����ABG=��D=90�㣬
���ABG+��ABF=90��+90��=180�㣬
��ˣ���G��B��F��ͬһ��ֱ���ϣ�
�ߡ�EAF=45����2+��3=��BAD-��EAF=90��-45��=45�㣮
�ߡ�1=��2�����1+��3=45�㣮
����GAF=��FAE��
��AG=AE��AF=AF
���GAF�ա�EAF��
��GF=EF����DE+BF=EF��
��2������Ǩ�ƣ�
��ͼ�ڣ���Rt��ABC��б�߷��۵õ���ADC����E��F�ֱ�ΪDC��BC���ϵĵ㣬�ҡ�EAF=$\frac{1}{2}$��DAB���Բ���DE��BF��EF֮���к�������ϵ����֤����IJ��룮
��3��������չ��
��ͼ�ۣ����ı���ABCD�У�AB=AD��E��F�ֱ�ΪDC��BC�ϵĵ㣬�����EAF=$\frac{1}{2}$��DAB���Բ��뵱��B���D����ʲô��ϵʱ����ʹ��DE+BF=EF����ֱ��д����IJ��루����˵�����ɣ���
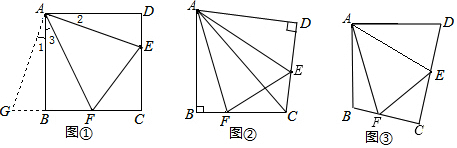
���� ��1���������ߣ�����ȫ�������Σ�֤����G��B��F��ͬһ��ֱ���ϣ���֤����GAF�ա�EAF���ɵý��ۣ�
��2��ͬ���������ߣ���ͼ�ڣ�����ADE��A˳ʱ����ת��BAD�Ķ�������ʱ��AD��AB�غϣ�֤����GAF�ա�EAF��ͬ�����Եó�EF=BG+BF=DE+BF��
��3������B���D�����D+��B=180��ʱ����ʹ��DE+BF=EF�������ǽ���ADE��A˳ʱ����ת��BAD�Ķ�����ͬ��֤����GAF�ա�EAF����EF=BG+BF=DE+BF��
��� �⣺��1������ADE�Ƶ�A˳ʱ����ת90��õ���ABG����ʱAB��AD�غϣ�����ת�ɵã�
AB=AD��BG=DE����1=��2����ABG=��D=90�㣬
���ABG+��ABF=90��+90��=180�㣬
��ˣ���G��B��F��ͬһ��ֱ���ϣ�
�ߡ�EAF=45��
���2+��3=��BAD-��EAF=90��-45��=45�㣮
�ߡ�1=��2��
���1+��3=45�㣮
����GAF=��FAE��
��AG=AE��AF=AF
���GAF�ա�EAF��
��GF=EF����DE+BF=EF��
�ʴ𰸣�FAE����EAF��GF��
��2����ͼ�ڣ�DE+BF=EF�������ǣ�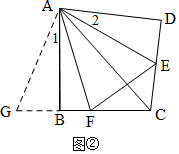
����ADE��A˳ʱ����ת��BAD�Ķ�������ʱ��AD��AB�غϣ�
����ת�ã�BG=DE����1=��2��AE=AG��
��ABG=��D=90�㣬
ͬ���ã���G��B��F��ͬһ��ֱ���ϣ�
�ߡ�EAF=$\frac{1}{2}$��DAB��
���BAF+��EAD=$\frac{1}{2}$��DAB��
���BAF+��GAB=$\frac{1}{2}$��DAB��
���GAF=��EAF��
��AE=AG��AF=AF��
���GAF�ա�EAF��
��EF=GF��
��EF=BG+BF=DE+BF��
��3������B���D�����D+��B=180��ʱ����ʹ��DE+BF=EF�������ǣ�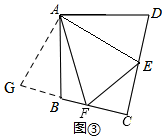
����ADE��A˳ʱ����ת��BAD�Ķ�������ʱ��AD��AB�غϣ�
����ת�ã�BG=DE����GAB=��DAE��AE=AG��
��ABG=��D��
�ߡ�D+��ABC=180��
���ABC+��ABG=180��
���G��B��F��ͬһ��ֱ���ϣ�
�ߡ�EAF=$\frac{1}{2}$��DAB��
���BAF+��EAD=$\frac{1}{2}$��DAB��
���BAF+��GAB=$\frac{1}{2}$��DAB��
���GAF=��EAF��
��AE=AG��AF=AF��
���GAF�ա�EAF��
��EF=GF��
��EF=BG+BF=DE+BF��
���� �������ı��ε��ۺ��⣬�����������ε����ʡ�������ȫ�ȵ����ʺ��ж���������������ȵ�˼�룬ͨ����ת�����Σ�������ת��������֤����һ��������ȫ�ȣ�������߶εĺͲ����⣮

 ��ڽ��ȫ������ϵ�д�
��ڽ��ȫ������ϵ�д�| A�� | 30m | B�� | 40m | C�� | 50m | D�� | 70m |
| A�� | $\frac{2}{{\sqrt{2}}}$ | B�� | $\root{3}{2}$ | C�� | $\sqrt{0.5}$ | D�� | $\sqrt{8}$ |
| A�� | -22=4 | B�� | |-$\sqrt{2}$|=$\sqrt{2}$ | C�� | $\sqrt{4}$=��2 | D�� | -|-2|=2 |
 ��ƽ��ֱ������ϵxOy�У���һ��C������C�ֱ���CA��x�ᣬCB��y�ᣬ��A��B�Ǵ��㣮
��ƽ��ֱ������ϵxOy�У���һ��C������C�ֱ���CA��x�ᣬCB��y�ᣬ��A��B�Ǵ��㣮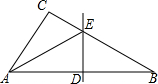 ��ͼ����ABC�У���C=90�㣬��AB�Ĵ�ֱƽ���߽�AB��AC�߷ֱ�Ϊ��D����E������BE����AB=10��BC=6�����ACE���ܳ���14��
��ͼ����ABC�У���C=90�㣬��AB�Ĵ�ֱƽ���߽�AB��AC�߷ֱ�Ϊ��D����E������BE����AB=10��BC=6�����ACE���ܳ���14��