题目内容
20.已知x是最大的负整数,y,z是有理数且满足$|\begin{array}{l}{z+2}\\{\;}\end{array}|$+(2y+3z)2=0,求$\frac{2xy+z}{{x}^{2}{-y}^{2}+4}$的值.分析 首先利用x是最大的负整数,y,z是有理数且满足$|\begin{array}{l}{z+2}\\{\;}\end{array}|$+(2y+3z)2=0求得x=-1,y=3,z=-2,进一步代入求得数值即可.
解答 解:∵x是最大的负整数,y,z是有理数且满足$|\begin{array}{l}{z+2}\\{\;}\end{array}|$+(2y+3z)2=0,
∴x=-1,z+2=0,2y+3z=0,
解得x=-1,y=3,z=-2,
∴$\frac{2xy+z}{{x}^{2}{-y}^{2}+4}$=$\frac{-6-2}{1-9+4}$=2.
点评 此题考查代数式求值,非负数的性质,代入数值计算注意字母与数值的对应以及符号的判定.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
5. 弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )
弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )
 弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )
弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数关系,图象如图所示,则弹簧本身的长度是( )| A. | 20cm | B. | 12.5cm | C. | 10cm | D. | 9cm |
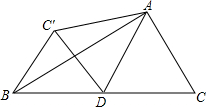 如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.
如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.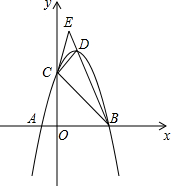 如图,已知抛物线y=-x2+bx+c交x轴于A(-1,0)、B(3,0)两点,交y轴于C点,抛物线的顶点为D,连接AC、BD并延长交于点E,连接BC,CD.
如图,已知抛物线y=-x2+bx+c交x轴于A(-1,0)、B(3,0)两点,交y轴于C点,抛物线的顶点为D,连接AC、BD并延长交于点E,连接BC,CD.