题目内容
10.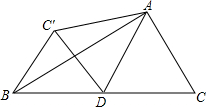 如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.
如图△ABC中,AD为底边上的中线,∠ADC=60°,BC=4,将△ADC沿AD翻折与△ADC′重合,则BC′=2.
分析 由三角形中线的定义可知:BD=DC=2,由翻折的性质可知CD=C′D=2,∠ADC=∠ADC′=60°,从而可求得∠C′DB=60°,C′D=DB,于是得到△BDC′为等边三角形.所以BC′=2.
解答 解:∵AD为底边上的中线,
∴BD=DC=2.
由翻折的性质可知:CD=C′D=2,∠ADC=∠ADC′=60°.
∴∠C′DB=60°,C′D=DB.
∴△BDC′为等边三角形.
∴BC′=BD=DC′=2.
故答案为:2.
点评 本题主要考查的是翻折的性质、中线的定义、等边三角形的性质和判定,证得△BDC′为等边三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.有五个编号分别是Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ的长方形,大小如表:
(1)通过计算,说明这五个长方形的周长相等;
(2)通过计算,说明长方形Ⅳ、Ⅴ的面积不可能最大.
| 长方形 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 长度 | 5 | 4 | 3 | 2 | 1 |
| 宽度 | x | x+1 | x+2 | x+3 | x+4 |
(2)通过计算,说明长方形Ⅳ、Ⅴ的面积不可能最大.
 小明平时爱动脑筋,深受老师喜爱,今天是小明的生日,老师想考小明,特地准备了一个三角形大蛋糕作为礼物,让小明只切三刀,把大蛋糕分成六等份,小明刚学完有关三角形中线的知识,动了一下脑筋,就把问题解决了,你知道小明如何解决的吗?
小明平时爱动脑筋,深受老师喜爱,今天是小明的生日,老师想考小明,特地准备了一个三角形大蛋糕作为礼物,让小明只切三刀,把大蛋糕分成六等份,小明刚学完有关三角形中线的知识,动了一下脑筋,就把问题解决了,你知道小明如何解决的吗?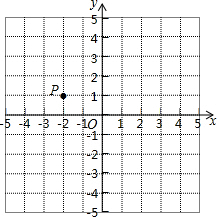 已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理)
已知P(-2,1).(第(1)(2)要求保留必要的作图轨迹和简单的说理) 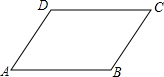 已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.
已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.