题目内容
4.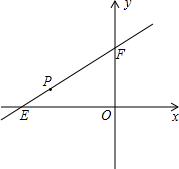 如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点.
如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点.(1)求k的值;
(2)若△OPE的面积为2,求点P的坐标.
分析 (1)将点E的坐标代入一次函数解析式中,即可得出关于k的一元一次方程,解方程即可得出结论;
(2)结合(1)中得k值可得出一次函数解析式,由点E的坐标可得出线段OE的长度,根据三角形的面积公式可求出点P的纵坐标,将点P的纵坐标代入一次函数解析式中即可求出点P的横坐标,由此即可得出结论.
解答 解:(1)将点E(-4,0)代入到y=kx+3中,
得:0=-4k+3=0,
解得:k=$\frac{3}{4}$.
(2)∵k=$\frac{3}{4}$,
∴直线EF的解析式为:y=$\frac{3}{4}$x+3.
∵点E的坐标为(-4,0),
∴OE=4,
∴S△OPE=$\frac{1}{2}$OP•yE=$\frac{1}{2}$×4yE=2,
∴yE=1.
令y=$\frac{3}{4}$x+3中y=1,则1=$\frac{3}{4}$x+3,
解得:x=-$\frac{8}{3}$.
故当△OPE的面积为2时,点P的坐标为(-$\frac{8}{3}$,1).
点评 本题考查了一次函数图象上点的坐标特征、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)利用待定系数法求出k值;(2)根据三角形的面积公式求出P点的纵坐标.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
14.使二次根式$\sqrt{x-2}$有意义的x的取值范围是( )
| A. | x>2≥2 | B. | x≥2 | C. | x<2 |
9.已知地球上海洋面积为316 000 000km2,数据316 000 000用科学记数法表示为( )
| A. | 3.61×109 | B. | 3.61×108 | C. | 3.61×107 | D. | 3.61×106 |
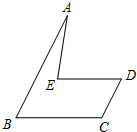 如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是80°.
如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是80°.