题目内容
15.先化简:($\frac{1}{x-1}$-$\frac{1}{x+1}$)÷$\frac{x}{{x}^{2}-x}$,再从-2<x<3的范围内选取一个合适的整数代入求值.分析 先算括号里面的,再算除法,根据-2<x<3选出合适的x的值代入原式进行计算即可.
解答 解:原式=$\frac{x+1-x+1}{(x-1)(x+1)}$•$\frac{x(x-1)}{x}$
=$\frac{2}{(x-1)(x+1)}$•$\frac{x(x-1)}{x}$
=$\frac{2}{x+1}$,
当x=2时,原式=$\frac{2}{3}$(x不能取0,1,-1).
点评 本题考查的是分式的化简求值,在解答此类题目时要注意x的取值保证分式有意义.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
5.下列说法中,正确的是( )
| A. | 不可能事件发生的概率为0 | |
| B. | 随机事件发生的概率为$\frac{1}{2}$ | |
| C. | 概率很小的事件不可能发生 | |
| D. | 投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 |
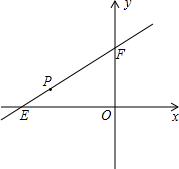 如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点.
如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点.