题目内容
19.解下列不等式:(1)3x-1<7-x
(2)$\frac{3x-2}{5}$≥$\frac{2x+1}{3}$-1.
分析 (1)先移项及合并同类项,然后系数化为1即可解答本题;
(2)先去分母,然后去括号、移项及合并同类项、系数化为1,即可解答本题.
解答 解:(1)3x-1<7-x,
移项及合并同类项,得
4x<8
系数化为1,得
x<2,
故原不等式的解集是:x<2;
(2)$\frac{3x-2}{5}$≥$\frac{2x+1}{3}$-1
不等式两边同乘以15,得
3(3x-2)≥5(2x+1)-15
去括号,得
9x-6≥10x+5-15
移项及合并同类项,得
-x≥-4
系数化为1,得
x≤4,
故原不等式的解集是x≤4.
点评 本题考查解一元一次不等式,解题的关键是明确解一元一次不等式的方法.

练习册系列答案
相关题目
8.如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为( )
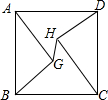

| A. | $\frac{8\sqrt{3}}{5}$ | B. | 2$\sqrt{2}$ | C. | $\frac{14}{5}$ | D. | 10-5$\sqrt{2}$ |
9.小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
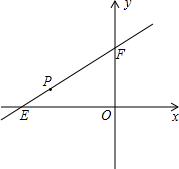 如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点.
如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点.