题目内容
12.先化简,再求值:($\frac{1}{a-b}$+$\frac{1}{a+b}$)÷$\frac{{a}^{2}b}{{a}^{2}-{b}^{2}}$,其中a=$\sqrt{2}$+1,b=$\sqrt{2}$-1.分析 先计算括号内,把除法化为乘法,最后代入计算即可.
解答 解:原式=$\frac{a+b+a-b}{(a+b)(a-b)}$÷$\frac{{a}^{2}b}{(a+b)(a-b)}$=$\frac{2a}{(a+b)(a-b)}$$•\frac{(a+b)(a-b)}{{a}^{2}b}$=$\frac{2}{ab}$,
∵a=$\sqrt{2}$+1,b=$\sqrt{2}$-1,
∴原式=$\frac{2}{(\sqrt{2}+1)(\sqrt{2}-1)}$=2.
点评 本题考查分式的化简求值、因式分解等知识,解题的关键是灵活运用分式的混合运算法则,代入计算时注意符号问题,学会应用公式,属于中考常考题型.

练习册系列答案
相关题目
2.分式$\frac{-{x}^{2}}{{x}^{2}+1}$的值为负,则x的取值范围是( )
| A. | 任意实数 | B. | x≠0 | C. | x≠0且x≠±1 | D. | x>0 |
17.直线y=kx+b交坐标轴于A(-8,0),B(0,13)两点,则不等式kx+b≥0的解集为( )
| A. | x≥-8 | B. | x≤-8 | C. | x≥13 | D. | x≤13 |
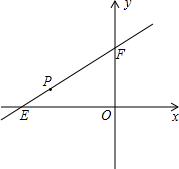 如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点.
如图,直线y=kx+3与x轴,y轴分别相交于点E,F,点E的坐标为(-4,0),点P(x,y)是线段EF上的一点. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.