题目内容
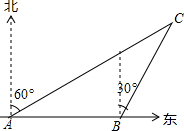 如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?
如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东30°方向.已知以小岛C为中心,周围10海里内有暗礁,问这艘渔船继续向东追赶鱼群是否有触礁的危险?考点:解直角三角形的应用-方向角问题
专题:
分析:根据题意可知,实质是比较C点到AB的距离与10的大小.因此作CD⊥AB于D点,求CD的长.
解答: 解:作CD⊥AB于D,
解:作CD⊥AB于D,
根据题意,AB=30×
=20(海里),∠CAD=30°,∠CBD=60°,
在Rt△ACD中,AD=
=
CD,
在Rt△BCD中,BD=
=
CD,
∵AB=AD-BD,
∴
CD-
CD=20(海里),
解得:CD=10
>10,
所以不可能.
 解:作CD⊥AB于D,
解:作CD⊥AB于D,根据题意,AB=30×
| 2 |
| 3 |
在Rt△ACD中,AD=
| CD |
| tan30° |
| 3 |
在Rt△BCD中,BD=
| CD |
| tan60° |
| ||
| 3 |
∵AB=AD-BD,
∴
| 3 |
| ||
| 3 |
解得:CD=10
| 3 |
所以不可能.
点评:本题考查了解直角三角形的应用,“化斜为直”是解三角形的常规思路,常需作垂线(高),构造直角三角形.原则上不破坏特殊角(30°、45°、60°).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若△ABC∽△DEF,且△ABC与△DEF的相似比为2:3,则S△ABC:S△DEF的值是( )
| A、2:3 | B、3:2 |
| C、4:9 | D、9:4 |
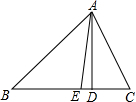 己知:如图,在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC.
己知:如图,在△ABC中,∠C>∠B,AD⊥BC于D,AE平分∠BAC. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,求△AEF的周长.
如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,求△AEF的周长.