题目内容
已知△ABC与△DEF的相似比为2：3，则△ABC与△DEF的面积比为 ．
考点：相似三角形的性质
专题：
分析：直接根据相似三角形的性质即可得出结论．
解答：解：∵△ABC∽△DEF，且△ABC与△DEF的相似比为2：3，
∴S△ABC：S△DEF=（
）2=4：9．
故答案为：4：9．
∴S△ABC：S△DEF=（
| 2 |
| 3 |
故答案为：4：9．
点评：本题考查的是相似三角形的性质，熟知相似三角形面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
相关题目
如图，已知△ABC≌△ADE，试证明：∠1=∠B+∠C．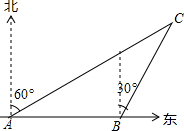
如图，一艘渔船以30海里/h的速度由西向东追赶鱼群．在A处测得小岛C在船的北偏东60°方向；40min后渔船行至B处，此时测得小岛C在船的北偏东30°方向．已知以小岛C为中心，周围10海里内有暗礁，问这艘渔船继续向东追赶鱼群是否有触礁的危险？
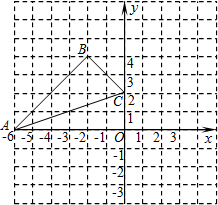如图，在直角坐标系中，△ABC的三个顶点的坐标分别为A（-6，0），B（-2，4），C（0，2）．画出△ABC的两个位似图形△A′B′C′，△A″B″C″，同时满足下列两个条件：
如图，AB是⊙O的一条弦（非直径），作直径CD，使CD⊥AB，则图中有（ ）对相等的不重叠的弧．| A、2 | B、3 | C、4 | D、5 |
下列计算正确的是（ ）
| A、（-1）0=-1 | ||
| B、（-1）-1=1 | ||
C、2a-3=
| ||
D、（-a5）÷（-a）7=
|