题目内容
20.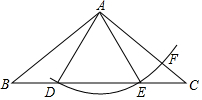 如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF.
如图,在△ABC中,AB=AC,D在边BC上,以A为圆心,AD长为半径画圆弧,交边BC的另一点E,交边AC于F,连接AE,EF.(1)求证:△ABD≌△ACE;
(2)若∠ADB=3∠CEF,请判断EF与AB有怎样的位置关系?并说明理由.
分析 (1)根据全等三角形的判定定理得到△ABD≌△ACD;
(2)根据已知条件得到∠AEF=2CEF,根据等腰三角形的性质得到∠AFE=∠AEF=2∠CEF,等量代换得到∠CEF=∠C,根据全等三角形的性质得到∠B=∠C,于是得到结论;
解答 证明:(1)由题意可知AD=AE=AF,
∴∠ADE=∠AED,
∴∠ADB=∠AEC,
∵AB=AC,
∴∠B=∠C,
在△ABD和△ACD中,$\left\{\begin{array}{l}{∠ADB=∠AEC}\\{∠B=∠C}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACD;
(2)∵∠ADB=∠AEC,∠ADB=3∠CEF,
∴∠AEF=2∠CEF,
∵AE=AF,
∴∠AFE=∠AEF=2∠CEF,
∴∠CEF=∠C,
∵△ABD≌△ACD,
∴∠B=∠C,
∴∠CEF=∠B,
∴EF∥AB.
点评 本题考查了直线与圆的位置关系,全等三角形的判断和性质,平行线的判定,熟练掌握全等三角形的判断和性质是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
11.抛物线y=x2+2x+m-1与x轴有交点,则m的取值范围是( )
| A. | m≤2 | B. | m<-2 | C. | m>2 | D. | 0<m≤2 |
15. 如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )
如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )
 如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )
如图,正方形ABCD中,AB=2,E为BC中点,两个动点M和N分别在边CD和AD上运动且MN=1,若△ABE与以D、M、N为顶点的三角形相似,则DM为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{3}$或$\frac{2}{3}$ | D. | $\frac{\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$ |
5.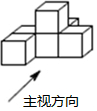 由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
 由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )| A. | 左视图与主视图相同 | B. | 俯视图与主视图相同 | ||
| C. | 左视图与俯视图相同 | D. | 三个视图都相同 |
12.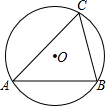 如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )
如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )
 如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )
如图,已知⊙O的直径为10,锐角△ABC内接于⊙O,BC=8,则∠A的正切值等于( )| A. | $\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
9. 已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )
已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )
 已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )
已知圆形纸片⊙O的直径为2,将其沿着两条互相垂直的直径折叠,得到四层的扇形,将最上的一层“撑”开来,“鼓”成一个无底的圆锥,则这个圆锥的高是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
4.已知关于x的一元一次方程(a+3)x|a|-2+6=0,则a的值为( )
| A. | 3 | B. | -3 | C. | ±3 | D. | ±2 |