题目内容
7.已知:?ABCD的对角线相交于O,EF经过O点且与AB交于E,与CD交于F,G,H分别是AO、CO的中点.求证:四边形EHFG是平行四边形.
分析 根据平行四边形的性质得出BO=DO,AO=CO,AB=CD,AB∥CD,求出∠EAO=∠FCO,根据ASA推出△EAO≌△FCO,根据全等得出EO=FO,求出GO=HO,根据平行四边形的判定得出即可.
解答 证明:如图,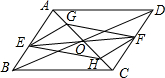
∵四边形ABCD为平行四边形,
∴BO=DO,AO=CO,AB=CD,AB∥CD,
∴∠EAO=∠FCO,
在△AEO和△CFO中,
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠FOC}\end{array}\right.$,
∴△EAO≌△FCO(ASA),
∴EO=FO,
又∵G、H分别为OA、OC的中点,
∴GO=HO,
∴四边形EHFG是平行四边形.
点评 本题考查了平行四边形的判定与性质,熟练掌握性质定理和判定定理是解题的关键.平行四边形的五种判定方法与平行四边形的性质相呼应,每种方法都对应着一种性质,在应用时应注意它们的区别与联系.

练习册系列答案
相关题目
18.已知点D与点A(-2,0),B(0,4),C(a,a)是一平行四边形的四个顶点,则CD长的最小值为( )
| A. | 4 | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
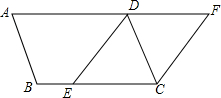 如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.
如图,?ABCD,点E是BC边的一点,将边AD延长至点F,使∠AFC=∠DEC,连接CF、DE.