题目内容
6．
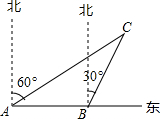如图所示，一艘渔船正以30海里/时的速度由西向东追赶鱼群，自A处经半小时到达B处，在A处看见小岛C在船的北偏东60°的方向上，在B处看见小岛C在船的北偏东30°的方向上，已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区，则这艘船继续向东追赶鱼群，是否有进入危险区域的可能？
分析 根据题意实质是比较C点到AB的距离与10的大小．因此作CD⊥AB于D点，求CD的长．
解答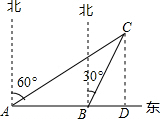 
解：作CD⊥AB于D，
根据题意，AB=30×$\frac{1}{2}$=15，∠CAD=30°，∠CBD=60°，
在Rt△ACD中，AD=$\frac{CD}{tan30°}$=$\sqrt{3}$CD，
在Rt△BCD中，BD=$\frac{CD}{tan60°}$=$\frac{\sqrt{3}}{3}$CD，
∵AB=AD-BD，
∴$\sqrt{3}$CD-$\frac{\sqrt{3}}{3}$CD=15，
CD=$\frac{45\sqrt{3}}{2}$＞10，
所以不可能．
点评 本题考查了解直角三角形的应用，“化斜为直”是解三角形的常规思路，常需作垂线（高），构造直角三角形．原则上不破坏特殊角（30°、45°、60°）．
练习册系列答案
相关题目
在平面直角坐标系中，一次函数的图象与坐标轴围成的三角形，叫做此一次函数的坐标三角形．例如，图中的一次函数的图象与x，y轴分别交于点A，B，则△OAB为此函数的坐标三角形．
11．下列各式从左到右的变形，正确的是（ ）
| A． | $\frac{y}{x}$=$\frac{{y}^{2}}{{x}^{2}}$ | B． | $\frac{y}{x}$=$\frac{yz}{xz}$（z≠0） | C． | $\frac{y}{x}$=$\frac{y-m}{x-m}$ | D． | $\frac{y}{x}$=$\frac{y+n}{x+n}$（n≠0） |
