题目内容
14. 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.(1)求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长;
(2)求此三角形面积.
分析 (1)先求函数y=$-\frac{3}{4}$x+3与x、y轴的交点坐标,再求三角形的三边长;
(2)根据三角形的面积公式解答即可.
解答 解:(1)由题意可得:A(4,0)B(0,3),
所以OA=4,OB=3,
在RT△AOB中,AB=$\sqrt{{4}^{2}+{3}^{2}}=5$;
(2)${S}_{△AOB}=\frac{1}{2}×3×4=6$.
点评 本题考查了一次函数问题,本题中根据一次函数和坐标轴的交点坐标,求坐标三角形的三边长是解题的基础.

练习册系列答案
相关题目
4.在△ABC中,∠C=90°,若c=10,a:b=3:4,则ab的值( )
| A. | 30 | B. | 40 | C. | 12 | D. | 48 |
5. 已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
 已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )| A. | -a<-b<a<b | B. | a<-b<b<-a | C. | -b<a<-a<b | D. | a<b<-b<-a |
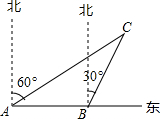 如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?
如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?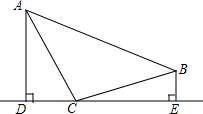 如图,点C在DE上,AC=BC,AD⊥DE于D,BE⊥DE于E,AD=CE.求证:AC⊥BC.
如图,点C在DE上,AC=BC,AD⊥DE于D,BE⊥DE于E,AD=CE.求证:AC⊥BC.