题目内容
1.解方程组(1)$\left\{\begin{array}{l}2x+y=5,\;\;\;\\ 3x-2y=4.\;\;\end{array}\right.$
(2)$\left\{\begin{array}{l}2x-3y-2=0\\ \frac{2x-3y+5}{7}+2y=9\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{2x+y=5①}\\{3x-2y=4②}\end{array}\right.$,
①×2+②得:7x=14,即x=2,
把x=2代入①得:y=1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{2x-3y=2①}\\{2x+11y=58②}\end{array}\right.$,
②-①得:14y=56,即y=4,
把y=4代入①得:x=7,
则方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列数轴画法正确的是( )
| A. |  | B. |  | C. |  | D. |  |
12.方程x(x-1)=x的解是( )
| A. | x=0 | B. | x=0、x=1 | C. | x=0和x=2 | D. | x=0或x=2 |
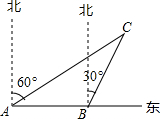 如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?
如图所示,一艘渔船正以30海里/时的速度由西向东追赶鱼群,自A处经半小时到达B处,在A处看见小岛C在船的北偏东60°的方向上,在B处看见小岛C在船的北偏东30°的方向上,已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,则这艘船继续向东追赶鱼群,是否有进入危险区域的可能?