题目内容
1.四川雅安芦山县发生7.0级大地震,重庆市政府从各个医院抽调骨干医生共8名组成抗震救灾医疗组,并决定用两辆小车火速把这些骨干医生送往芦山县城参加救灾.已知每辆车含司机在内限乘5人,出发后,由于余震山体滑坡,造成其中一辆车在距芦山县城19.5千米的地方发生故障,此时离抗震指挥部规定到达的时间还有54分钟,这时唯一可利用的车是其中的另一辆,由于路况限制,这辆车的平均速度是60千米/小时,如果医生步行,则步行的平均速度是5千米/小时.(1)医疗小组负责人立即决定:搭乘发生故障小车的4个人下车步行,另一辆车将车内4人送到芦山县城后,立即返回接步行的4个人到芦山县城.你认为:按照这个方案行进,能保证整个医疗小组在规定时间前全部赶到芦山县城吗?请通过计算说明你的理由.
(2)在题目设定条件下,请你为医疗小组设计一种与(1)不同的、能保证整个医疗小组在规定时间前赶到芦山县城的行走方案,并通过计算说明方案的可行性.
分析 (1)根据题意可知,一辆车发生故障时,没有发生故障的车与医生是同向行驶问题,到没有发生故障的车再返回接步行的医生是相向行驶问题,然后接到医生再返回县城是单向行驶问题,只要将这三段的时间计算出来求出它们的和与45分钟做比较即可解答本题;
(2)设计的方案只要符合要求即可,步行的医生休息一段时间的路程正好是汽车行驶的这段路程的2倍,然后求出这段时间即可解答命题.
解答 解:(1)按照这个方案行进,能保证整个医疗小组在规定时间前全部赶到芦山县城.
理由:由题意可得,
设没出故障的车从距芦山县城19.5千米到县城用的时间为t1小时,再次与步行医生相遇用的时间为t2小时,相遇后再返回县城用的时间为t3小时,
${t}_{1}=\frac{19.5}{60}=\frac{13}{40}$,
${t}_{2}=\frac{19.5-5×\frac{13}{40}}{60+5}$=$\frac{143}{520}$,
${t}_{3}=\frac{19.5-5×\frac{13}{40}-5×\frac{143}{520}}{60}$=$\frac{143}{520}$,
${t}_{1}+{t}_{2}+{t}_{3}=\frac{13}{40}+\frac{143}{520}+\frac{143}{520}=\frac{91}{104}$小时=52.5分,
∵52.5<54,
∴按照这个方案行进,能保证整个医疗小组在规定时间前全部赶到芦山县城;
(2)方案是:搭乘发生故障小车的4个人下车步行,中间休息2分钟,另一辆车将车内4人送到芦山县城后,立即返回接步行的4个人到芦山县城.
没出故障的车从距芦山县城19.5千米到最后全部医生到达县城用的时间为:52.5+$\frac{\frac{2}{60}×5×2}{60}×60=52.5+\frac{1}{3}$=52.888<54,
故此方案可行.
点评 本题考查一元一次方程的应用,解题的关键是明确题意,列出相应的方程,找出所求问题需要的条件.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 如图,一次函数的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(m,6)和点B(4,-3).
如图,一次函数的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(m,6)和点B(4,-3). 如图,抛物线y=$\frac{1}{2}$x2+bx+c与直线l:y=kx+m交于A(4,2)、B(0,-1)两点.
如图,抛物线y=$\frac{1}{2}$x2+bx+c与直线l:y=kx+m交于A(4,2)、B(0,-1)两点.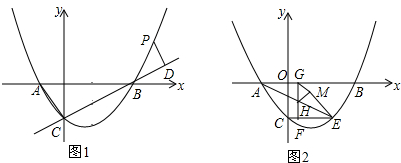
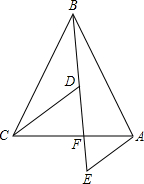 如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.
如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系. 四条直线AB,CD,EF,GH相交成如图所示的形状,那么与∠FPD构成同位角的角是∠HQD、∠FMB.
四条直线AB,CD,EF,GH相交成如图所示的形状,那么与∠FPD构成同位角的角是∠HQD、∠FMB.