题目内容
10.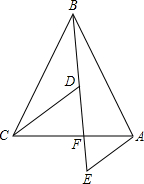 如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.
如图,在△ABC中,BC=BA,点F是AC上一点.点D是BF上一点,且∠CDF=∠CBA,AE∥CD交BF延长线于E.探究线段BD与EA的数量关系.
分析 在线段BE上取一点M,使得AM=AE,由∠CDE=∠ABC得∠DCB+∠CBD=∠CBD+∠ABD故∠BCD=∠ABD,再由CD∥AE推出∠BDC=∠AMB即可证明△BDC≌△AMB得出结论.
解答 解:结论:BD=AE,理由如下:
在线段BE上取一点M,使得AM=AE,
∵CD∥AE,
∴∠CDE=∠E,
∵AM=AE,
∴∠E=∠AME=∠CDE,
∵∠BDC=180°-∠CDE,∠AMB=180°-AME,
∴∠BDC=∠AMB,
∵∠CDE=∠ABC,
∴∠DCB+∠CBD=∠CBD+∠ABD,
∴∠BCD=∠ABD,
在△BDC和△AMB中,
$\left\{\begin{array}{l}{∠BCD=∠ABM}\\{∠CDB=∠AMB}\\{BC=BA}\end{array}\right.$,
∴△BDC≌△AMB,
∴BD=AM,
∵AM=AE,
∴BD=AE.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、平行线的性质等知识,添加辅助线构造全等三角形是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.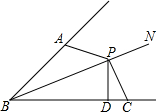 已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.
已知如图:∠ABP=∠CBP,P为BN上一点,且PD⊥BC于点D,∠BAP+∠BCP=180°,求证:AB+BC=2BD.

 如图,写出图中所有同位角、内错角、同旁内角.
如图,写出图中所有同位角、内错角、同旁内角.