题目内容
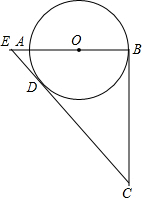如图所示，CB、CD分别切圆心O于点B、D，AB为圆心O的直径，延长BA交CD的延长线于点E，求证：ED•EC=EO•EB．考点：切线的性质,相似三角形的判定与性质
专题：证明题
分析：连接OD，证明Rt△ODE∽Rt△CBE，则由对应边的比例相等可得比例式，化成乘积式即可．
解答：
证明：连接OD，
∵CB、CD为圆的切线，
∴OD⊥CD，AB⊥BC，
∴∠ODE=∠EBC=90°，
且∠E为公共角，
∴Rt△ODE∽Rt△CBE，
∴
=
，
∴ED•EC=EO•EB．
证明：连接OD，
∵CB、CD为圆的切线，
∴OD⊥CD，AB⊥BC，
∴∠ODE=∠EBC=90°，
且∠E为公共角，
∴Rt△ODE∽Rt△CBE，
∴
| ED |
| EB |
| EO |
| EC |
∴ED•EC=EO•EB．
点评：本题主要考查切线的性质和相似三角形的判定和性质，解题的关键是构造三角形证明相似．
练习册系列答案
相关题目
如图，四边形ABCD是⊙O的内接四边形，且AC⊥BD，OF⊥AB，垂足分别为E、F，请问OF与CD有怎样的数量关系？
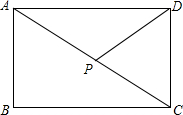如图，矩形ABCD中，AB=3，BC=4，点P是对角线AC上的动点（不与A、C重合），设AP=x，S△CDP=y．
如图，OC平分∠AOB，若∠BOC=28°32′，则∠AOB=