题目内容
已知抛物线y=-x2+2x+8，求它与x轴的交点和抛物线顶点的坐标．
考点：抛物线与x轴的交点
专题：
分析：首先把已知函数解析式配方，即可求出抛物线的顶点坐标；令y=0即可求出它与x轴的交点．
解答：解：∵y=-x2+2x+8，
=-（x-1）2+9，
∴抛物线顶点的坐标为（1，9）；
令y=0，则0=-x2+2x+8，
解得：x=4或-2，
∴它与x轴的交点坐标为（4，0）或（-2，0）．
=-（x-1）2+9，
∴抛物线顶点的坐标为（1，9）；
令y=0，则0=-x2+2x+8，
解得：x=4或-2，
∴它与x轴的交点坐标为（4，0）或（-2，0）．
点评：此题主要考查了抛物线与x轴的交点、函数图象的性质及二次函数的三种形式，都是二次函数的基础知识，要求学生熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
半径为R的⊙O1和半径为r的⊙O2外切于点P，AB为两圆的外公切线，切点为A、B，连心线O2O1交圆⊙O1于C，交⊙O2于D，CA与DB的延长线相交于Q．若R=3r，求∠ABQ的度数．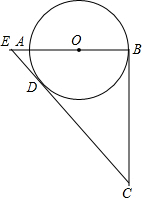
如图所示，CB、CD分别切圆心O于点B、D，AB为圆心O的直径，延长BA交CD的延长线于点E，求证：ED•EC=EO•EB．