题目内容
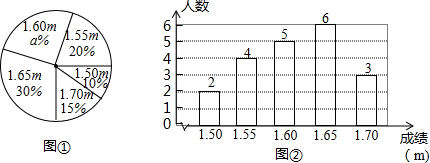
20.在一次中学生田径运动会上,根据参加男子跳高初赛运动员的成绩(单位:m),绘制出如下所示的条形统计图和扇形统计图,请根据统计图相关信息,解答下列问题:(1)求扇形统计图中a值;
(2)求男子跳高初赛成绩的平均数、众数和中位数.
分析 (1)根据题意列式计算即可;
(2)观察条形统计图求得平均数,根据众数,中位数的定义即可得到结论.
解答 (解:(1)根据题意得:1-20%-10%-15%-30%=25%;
则a的值是25;
(2)观察条形统计图得:
$\overline{x}$=$\frac{1.50×2+1.55×4+1.60×5+1.65×6+1.70×3}{2+4+5+6+3}$=1.61,
∵在这组数据中,1.65出现了6次,出现的次数最多,
∴这组数据的众数是1.65,
将这组数据从小到大排列,其中处于中间的两个数都是1.60,
则这组数据的中位数是1.60.
点评 此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题中的数据是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.用火柴棒搭的图形如图所示:
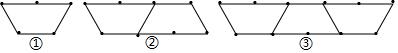
(1)若按这样的规律摆下去,请把表格补充完整:
(2)搭第几个图形需要2017根火柴棒?
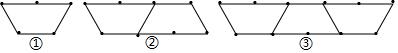
(1)若按这样的规律摆下去,请把表格补充完整:
| 图形标号 | ① | ② | ③ | ④ | ⑤ | … | n | … |
| 火柴棒数 | 5 | 9 | 13 | 17 | 21 | … | 4n+1 | … |
15.下列计算正确的是( )
| A. | 3$\sqrt{2}$×4$\sqrt{2}$=12$\sqrt{2}$ | B. | $\sqrt{(-3)^{2}}$=-3 | C. | ($\sqrt{8}$-$\sqrt{3}$)×$\sqrt{6}$=4$\sqrt{3}$-9$\sqrt{2}$ | D. | (4$\sqrt{2}$-3$\sqrt{6}$)÷2$\sqrt{2}$=2-$\frac{3}{2}$$\sqrt{3}$ |
5.已知反比例函数y=$\frac{6}{x}$,在下列结论中,错误的是( )
| A. | 图象位于第一、三象限 | B. | 图象必经过点(-2,-3) | ||
| C. | y随x的增大而增大 | D. | 若x>2,则y<3 |
9.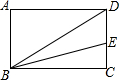 如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
 如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
如图,在矩形ABCD中,AB=3,BC=4,连结BD,作∠CBD的平分线交CD于点E,则CE的长度为( )| A. | $\frac{4}{3}$ | B. | 2 | C. | 3 | D. | 4 |
 如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为10.
如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为10. 如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.
如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.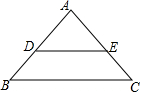 如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )
如图,在△ABC中,点D,E分别在AB,AC边上,且DE∥BC,若AD:DB=3:2,AE=6,则EC等于( )