题目内容
12. 如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.
如图,AB是⊙O的直径,⊙O与AC相交于点D,∠BAC=45°,AB=BC.(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为2cm,求图中阴影部分的面积.
分析 (1)先利用等腰三角形的性质得到∠BAC=∠C=45°,则∠ABC=90°,然后根据切线的判定定理可得到BC是⊙O的切线;
(2)连接BD,如图,利用圆周角定理得到∠ADB=90°,则根据等腰直角三角形的性质得到AD=CD=BD,所以弓形AD的面积与弓形BD的面积相等,则图中阴影部分的面积=$\frac{1}{2}$S△ABC,然后根据三角形的面积公式计算即可.
解答 (1)证明:∵AB=BC,
∴∠BAC=∠C=45°,
∴∠ABC=180°-∠BAC-∠C=90°,
∴AB⊥BC,
∴BC是⊙O的切线;
(2)解:连接BD,如图,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD=CD=BD,
∴$\widehat{AD}$=$\widehat{BD}$,
∴图中阴影部分的面积=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×$\frac{1}{2}$×AB×BC=$\frac{1}{2}$×$\frac{1}{2}$×4×4=4(cm2).
点评 本题考查了切线的判定与性质:圆的切线垂直于经过切点的半径.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”.也考查了等腰直角三角形的性质和不规则几何图形的面积的计算方法.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.下列根据等式的性质变形正确的是( )
| A. | 由-$\frac{1}{3}$x=$\frac{2}{3}$y,得x=2y | B. | 由5x-2=4x+2,得x=4 | ||
| C. | 由2x-1=3x,得x=1 | D. | 由3x-5=7,得3x=7-5 |
4.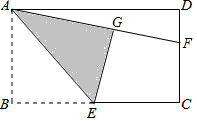 如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )
如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )
 如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )
如图,在矩形ABCD中,E是BC边的中点,将△ABE沿AE所在直线折叠得到△AGE,延长AG交CD于点F,已知CF=2,FD=1,则BC的长是( )| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{6}$ | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{3}$ |
1.下列计算中正确的是( )
| A. | 2a+3b=5ab | B. | a3+a3=2a3 | C. | 4a2-a2=3 | D. | (-a)3=a3 |
2.若-3xm+1y2016与2x2015yn是同类项,则|m-n|的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
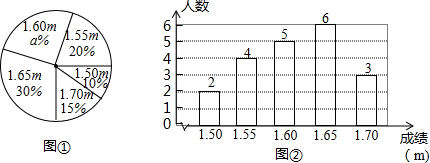




 如图,已知线段AB.
如图,已知线段AB.