题目内容
7.已知y是x的二次函数,当x=2时,y=-4,当y=4时,x恰为方程2x2-x-8=0的根.(1)解方程 2x2-x-8=0
(2)求这个二次函数的解析式.
分析 (1)利用公式法或配方法解方程即可;
(2)设这个方程的根为x1、x2,即当x=x1,x=x2时,y=4,可设抛物线解析式y=a(2x2-x-8)+4,再将x=2,y=-4代入求a即可.
解答 解:
(1)∵2x2-x-8=0,
∴a=2,b=-1c=-8,
∴△=1+64=65>0,
∴x1=$\frac{1+\sqrt{65}}{4}$,x2=$\frac{1-\sqrt{65}}{4}$;
(2)设方程2x2-x-8=0的根为x1、x2,则
当x=x1,x=x2时,y=4,可设y=a(2x2-x-8)+4,
把x=2,y=-4代入,得-4=a(2×22-2-8)+4,
解得a=4,
所求函数为y=4(2x2-x-8)+4,
即y=8x2-4x-28.
点评 本题综合考查了一元二次方程的根与二次函数图象上点的坐标的关系,巧妙地设二次函数解析式,用待定系数法求解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列命题中,正确的是( )
| A. | 长度相等的弧是等弧 | B. | 三点确定一个圆 | ||
| C. | 相等的圆心角所对的弧相等 | D. | 垂直弦的直径平分这条弦 |
2.若等腰三角形的一边长是2,另一边长是4,则它的周长为( )
| A. | 8 | B. | 10 | C. | 8或10 | D. | 不能确定 |
12.若等腰三角形的两边长分别为4和6,则它的周长是( )
| A. | 14 | B. | 15 | C. | 16 | D. | 14或16 |
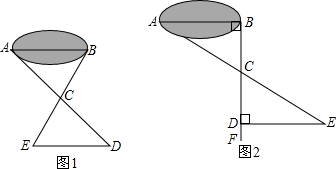 八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
八(3)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案: 如图,是2016年11月月历:
如图,是2016年11月月历: