题目内容
17.已知m=$\sqrt{n+31}$-$\sqrt{n-5}$+$\sqrt{5-n}$,x=$\frac{1}{\sqrt{m}+\sqrt{n}}$,y=$\frac{1}{\sqrt{m}-\sqrt{n}}$,则代数式x2+xy-y2的值为1-4$\sqrt{30}$.分析 先根据m=$\sqrt{n+31}$-$\sqrt{n-5}$+$\sqrt{5-n}$,求出n和m的值,然后求出x和y的值,代入代数式x2+xy-y2求解即可.
解答 解:∵m=$\sqrt{n+31}$-$\sqrt{n-5}$+$\sqrt{5-n}$,
∴$\left\{\begin{array}{l}{n-5≥0}\\{5-n≥0}\end{array}\right.$,
∴n=5,
m=$\sqrt{36}$=6,
∴x=$\frac{1}{\sqrt{6}+\sqrt{5}}$=$\sqrt{6}-\sqrt{5}$,y=$\frac{1}{\sqrt{6}-\sqrt{5}}$=$\sqrt{6}+\sqrt{5}$,
∴x2+xy-y2
=($\sqrt{6}-\sqrt{5}$)2+($\sqrt{6}-\sqrt{5}$)($\sqrt{6}+\sqrt{5}$)-($\sqrt{6}+\sqrt{5}$)2
=11-2$\sqrt{30}$+1-11-2$\sqrt{30}$
=1-4$\sqrt{30}$.
故答案为:1-4$\sqrt{30}$.
点评 本题考查了二次根式的化简求值,解答本题的关键在于根据m=$\sqrt{n+31}$-$\sqrt{n-5}$+$\sqrt{5-n}$,求出n和m的值,然后求出x和y的值,代入代数式x2+xy-y2求解.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
2.在有理数在数轴上的位置如图所示,则下列各式的符号为负的是( )


| A. | -a-b | B. | a+b | C. | -a3b3 | D. | a4b4 |
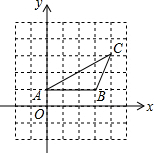 已知A(0,1),B(3,1),C(4,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为(-1,3)或(-1,-1)或(4,-1).
已知A(0,1),B(3,1),C(4,3),如果在平面直角坐标系中存在一点D,使得△ABD与△ABC全等,那么点D的坐标为(-1,3)或(-1,-1)或(4,-1).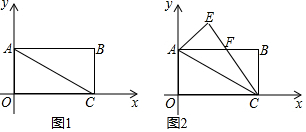
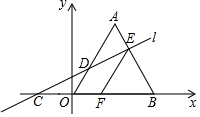 如图,在平面直角坐标系中,△AOB是边长为6的等边三角形,直线l与x轴、OA、AB分别交于点C、D、E,OC=AE.过点E作EF∥OA,交x轴于点F.
如图,在平面直角坐标系中,△AOB是边长为6的等边三角形,直线l与x轴、OA、AB分别交于点C、D、E,OC=AE.过点E作EF∥OA,交x轴于点F.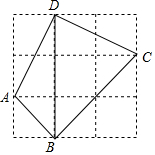 如图,在3×3的正方形网格中有一个四边形ABCD,若小正方形的边长为1,则sin∠ADB+cos∠DBC=$\frac{\sqrt{5}}{5}$+$\frac{\sqrt{2}}{2}$.
如图,在3×3的正方形网格中有一个四边形ABCD,若小正方形的边长为1,则sin∠ADB+cos∠DBC=$\frac{\sqrt{5}}{5}$+$\frac{\sqrt{2}}{2}$.