题目内容
据调查,某地区有100万人从事传统农业的非城镇居民,人均年收入5000元.为了增加这些非城镇居民的收入,当地政府积极引资建立各种加工企业,对当地的农产品进行深加工,同时吸收部分这些非城镇居民进入加工企业工作.据统计,如果有x万这些非城镇居民进入加工企业工作(x>0),那么剩下从事传统农业的非城镇居民的人均年收入将提高2x%,而进入加工企业工作的这些非城镇居民人均年收入为5000a元(a>0).
(1)若该地区在建立加工企业后从事传统农业的非城镇居民的年总收入刚好等于加工企业建立前全部非城镇居民的年总收入,求x的值;
(2)若0<x≤50,a=3.则当地政府应安排多少万非城镇居民进入加工企业工作,才能使这100万非城镇居民的人均年收入达到最大?其最大人均年收入为多少元?
(1)若该地区在建立加工企业后从事传统农业的非城镇居民的年总收入刚好等于加工企业建立前全部非城镇居民的年总收入,求x的值;
(2)若0<x≤50,a=3.则当地政府应安排多少万非城镇居民进入加工企业工作,才能使这100万非城镇居民的人均年收入达到最大?其最大人均年收入为多少元?
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)先根据题意得出一个关于x的不等关系:(100-x)•5000•(1+2x%)=100×5000,解此方程即得x的值;
(2)设安排x万非城镇居民进入加工企业工作,这100万非城镇居民的人均年收入为y元,利用已知分别表示出从事传统农业的非城镇居民和进入加工企业工作的这些非城镇居民人均年收入进而求出即可.
(2)设安排x万非城镇居民进入加工企业工作,这100万非城镇居民的人均年收入为y元,利用已知分别表示出从事传统农业的非城镇居民和进入加工企业工作的这些非城镇居民人均年收入进而求出即可.
解答:解:(1)根据题意,
(100-x)•5000•(1+2x%)=100×5000,
即x2-50x=0,
解得:x1=0(舍去),x2=50;
(2)设安排x万非城镇居民进入加工企业工作,这100万非城镇居民的人均年收入为y元,依据题意可得出:
y=
化简得:y=-x2+200x+5000=-(x-100)2+15000,
根据二次函数的图象知:当0<x≤50时,y随x增大而增大,
∴当x=50时,y有最大值为12500,故当地政府应安排50万非城镇居民进入加工企业工作,
才能使这100万非城镇居民的人均年收入达到最大,其最大人均年收入为12500元.
(100-x)•5000•(1+2x%)=100×5000,
即x2-50x=0,
解得:x1=0(舍去),x2=50;
(2)设安排x万非城镇居民进入加工企业工作,这100万非城镇居民的人均年收入为y元,依据题意可得出:
y=
| (100-x)×5000(1+2x%)+5000×3x |
| 100 |
化简得:y=-x2+200x+5000=-(x-100)2+15000,
根据二次函数的图象知:当0<x≤50时,y随x增大而增大,
∴当x=50时,y有最大值为12500,故当地政府应安排50万非城镇居民进入加工企业工作,
才能使这100万非城镇居民的人均年收入达到最大,其最大人均年收入为12500元.
点评:本题主要考查了函数模型的选择与应用,属于基础题.解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
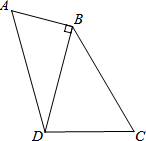 如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长.
如图,在四边形ABCD中,AB=2,∠A=∠C=60°,DB⊥AB于点B,∠DBC=45°,求BC的长.
 已知,如图,点B、E、F、C在同一条直线上,∠A=∠D,BE=CF,∠B=∠C.
已知,如图,点B、E、F、C在同一条直线上,∠A=∠D,BE=CF,∠B=∠C.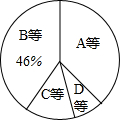 某校为了了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四个等级,并绘制成下面的频数分布表(表一)和扇形统计图.
某校为了了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四个等级,并绘制成下面的频数分布表(表一)和扇形统计图.