题目内容
4.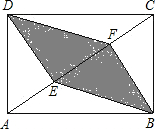 如图,一块矩形场地ABCD,现测得边长AB与AD之比为$\sqrt{2}$:1,DE⊥AC于点E,BF⊥AC于点F,连接BE,DF.现计划在四边形DEBF区域内种植花草.
如图,一块矩形场地ABCD,现测得边长AB与AD之比为$\sqrt{2}$:1,DE⊥AC于点E,BF⊥AC于点F,连接BE,DF.现计划在四边形DEBF区域内种植花草.(1)求证:AE=EF=CF.
(2)求四边形DEBF与矩形ABCD的面积之比.
分析 (1)根据题意可设AD=x,则AB=$\sqrt{2}$x,AC=$\sqrt{3}$x,利用△ADC的面积为定值可求DE的长,再根据勾股定理可求出AE,EF,CF的长,即可证明AE=EF=CF.
(2)由(1)中的数据分别计算出四边形DEBF与矩形ABCD的面积,再作比值即可.
解答 (1)证明:
矩形ABCD中,∠ADC=90°,设AD=x,则AB=$\sqrt{2}$x,AC=$\sqrt{3}$x,
∵DE⊥AC于点E,
∴DE=$\frac{x•\sqrt{2}x}{\sqrt{3}x}$=$\frac{\sqrt{6}}{3}$x,
在△ADE中,AE=$\sqrt{{x}^{2}-(\frac{\sqrt{6}}{3}x)^{2}}$=$\frac{\sqrt{3}}{3}$x,同理CF=$\frac{\sqrt{3}}{3}$x,EF=$\frac{\sqrt{3}}{3}$x,
∴AE=CF=EF;
(2)解:
S四边形DEBF=EF×DE=$\frac{\sqrt{3}}{3}$x•$\frac{\sqrt{6}}{3}$x=$\frac{\sqrt{2}}{3}$x2,
而S矩形ABCD=x×$\sqrt{2}$x=$\sqrt{2}$x2,
∴四边形DEBF与矩形ABCD的面积之比为1:3.
点评 本题考查了矩形的性质、勾股定理的运用以及四边形面积公式和矩形面积公式的运用,题目的综合性较强,计算量较大,是一道不错的中考题.

练习册系列答案
相关题目
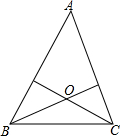 已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.
已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.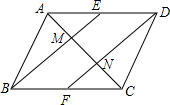 如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.请你结合上述条件,写出两个你认为正确且与M、N有关的结论:
如图,在平行四边形ABCD中E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.请你结合上述条件,写出两个你认为正确且与M、N有关的结论: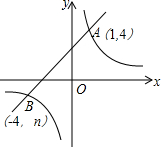 如图,反比例函数y=$\frac{k}{x}$(k≠0)的图象与一次函数y=x+b的图象交于A(1,4)、B(-4,n).
如图,反比例函数y=$\frac{k}{x}$(k≠0)的图象与一次函数y=x+b的图象交于A(1,4)、B(-4,n).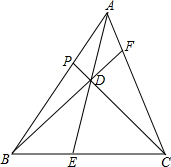 如图,在△ABC中,设E,F,P分别在边BC,CA,AB上,已知AE,BF,CP交于一点D,且$\frac{AD}{DE}$+$\frac{BD}{DF}$+$\frac{CD}{DP}$=n,则$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=n+2.
如图,在△ABC中,设E,F,P分别在边BC,CA,AB上,已知AE,BF,CP交于一点D,且$\frac{AD}{DE}$+$\frac{BD}{DF}$+$\frac{CD}{DP}$=n,则$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=n+2. 如图,菱形ABCD的边长为8cm,∠BAD=60°,则对角线AC的长为8$\sqrt{3}$cm.
如图,菱形ABCD的边长为8cm,∠BAD=60°,则对角线AC的长为8$\sqrt{3}$cm.