题目内容
5.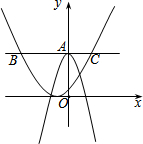 如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )
如图,在平面直角坐标系中,过点A与x轴平行的直线交抛物线y=$\frac{1}{3}{(x+1)^2}$于点B、C,线段BC的长度为6,抛物线y=-2x2+b与y轴交于点A,则b=( )| A. | 1 | B. | 4.5 | C. | 3 | D. | 6 |
分析 根据题意知点A(0,b),设点C(x1,b)、点B(x2,b),则x1、x2是方程$\frac{1}{3}{(x+1)^2}$=b的两根,根据BC长度可得x1-x2=6即(x1+x2)2-4x1x2=36,由韦达定理将x1+x2、x1x2代入求解可得.
解答 解:根据题意点A(0,b),设点C(x1,b)、点B(x2,b),
抛物线y=$\frac{1}{3}{(x+1)^2}$中,当y=b时,有$\frac{1}{3}{(x+1)^2}$=b,
即:x2+2x+1-3b=0,
∴x1+x2=-2,x1x2=1-3b,
∵BC=6,即x1-x2=6,
∴(x1-x2)2=36,即(x1+x2)2-4x1x2=36,
则:4-4(1-3b)=36,
解得:b=3,
故选:C.
点评 本题考查了二次函数性质,根据二次函数与一元二次方程间的关系,结合平行于x轴上的两点之间的距离是解决本题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
10.为了了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:
下列结论不正确的是( )
| 居民户数 | 1 | 3 | 2 | 4 |
| 月用电量(度/户) | 40 | 50 | 55 | 60 |
| A. | 众数是60 | B. | 平均数是54 | C. | 中位数是55 | D. | 方差是29 |
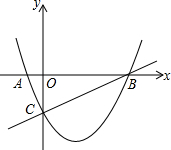 如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC,
如图:已知抛物线y=ax2-$\frac{3}{2}$x+c与x轴相交于A、B两点,并与直线y=$\frac{1}{2}$x-2交于B、C两点,其中点C是直线y=$\frac{1}{2}$x-2与y轴交点,连接AC, 如图,在矩形ABCD中,点E是CD上一点,AB=AE,BF⊥AE,垂足为F.求证:BF=BC.
如图,在矩形ABCD中,点E是CD上一点,AB=AE,BF⊥AE,垂足为F.求证:BF=BC.