题目内容
 如图,将一张圆形纸片沿互相垂直的两条半径OA、OB剪得两个扇形,并用这两个扇形围成两个圆锥的侧面,求这两个圆锥底面圆半径间的数量关系.
如图,将一张圆形纸片沿互相垂直的两条半径OA、OB剪得两个扇形,并用这两个扇形围成两个圆锥的侧面,求这两个圆锥底面圆半径间的数量关系.考点:圆锥的计算
专题:计算题
分析:设由面积为S1的扇形所围成的圆锥的底面圆的半径为r1,由面积为S2的扇形所围成的圆锥的底面圆的半径为r2,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr1=
,2πr2=
,然后求r1:r2即可.
| 90•π•OA |
| 180 |
| 270•π•OA |
| 180 |
解答:解:设由面积为S1的扇形所围成的圆锥的底面圆的半径为r1,由面积为S2的扇形所围成的圆锥的底面圆的半径为r2,
∵OA⊥OB,
∴∠AOB=90°,
∴2πr1=
,2πr2=
,
∴
=
,
即这两个圆锥底面圆半径之比为1:3.
∵OA⊥OB,
∴∠AOB=90°,
∴2πr1=
| 90•π•OA |
| 180 |
| 270•π•OA |
| 180 |
∴
| r1 |
| r2 |
| 1 |
| 3 |
即这两个圆锥底面圆半径之比为1:3.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆的母线长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
实数a、b在数轴上对应点的位置如图,则|a-b|-
的结果是( ) 
| a2 |

| A、2a-b | B、b-2a |
| C、b | D、-b |
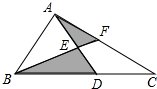 如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是
如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是 如图,点E是△ABC的内心,AE交△ABC的外接圆于点D,求证:BD=ED=CD.
如图,点E是△ABC的内心,AE交△ABC的外接圆于点D,求证:BD=ED=CD. 如图,点C是
如图,点C是