题目内容
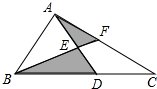 如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是
如图所示,阴影部分的面积是2cm2,AE=ED,BD=2DC,则△ABC的面积是考点:相似三角形的性质
专题:
分析:连接DF,设S△AEF=x,S△BDE=y,然后根据等底等高的三角形的面积相等表示出S△ABE、S△DEF,再根据等高的三角形的面积的比等于底边的比表示出S△CDF,然后求解即可.
解答: 解:如图,连接DF,设S△AEF=x,S△BDE=y,
解:如图,连接DF,设S△AEF=x,S△BDE=y,
∵阴影部分的面积是2cm2,
∴x+y=2cm2,
∵AE=ED,
∴S△ABE=y,S△DEF=x,
∵BD=2DC,
∴S△CDF=
S△BDF=
(x+y),
∴△ABC的面积=2x+2y+
(x+y)=
(x+y)=
×2=5cm2.
故答案为:5.
 解:如图,连接DF,设S△AEF=x,S△BDE=y,
解:如图,连接DF,设S△AEF=x,S△BDE=y,∵阴影部分的面积是2cm2,
∴x+y=2cm2,
∵AE=ED,
∴S△ABE=y,S△DEF=x,
∵BD=2DC,
∴S△CDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABC的面积=2x+2y+
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
故答案为:5.
点评:本题考查了三角形的面积,主要利用了等底等高的三角形的面积相等,等高的三角形的面积的比等于底边的比,作辅助线把三角形分割是解题的关键.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
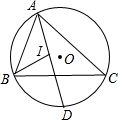 如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I.
如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于D,∠ABC的平分线交直线AD于I. 如图,将一张圆形纸片沿互相垂直的两条半径OA、OB剪得两个扇形,并用这两个扇形围成两个圆锥的侧面,求这两个圆锥底面圆半径间的数量关系.
如图,将一张圆形纸片沿互相垂直的两条半径OA、OB剪得两个扇形,并用这两个扇形围成两个圆锥的侧面,求这两个圆锥底面圆半径间的数量关系. 如图,在△ABC中,∠BAC=90°,∠B=30°,AC=6,AD⊥BC,交BC于点D,E为BC的中点,求AE的长.
如图,在△ABC中,∠BAC=90°,∠B=30°,AC=6,AD⊥BC,交BC于点D,E为BC的中点,求AE的长.