题目内容
18.计算$\frac{{{{({x+y})}^2}-{{({x-y})}^2}}}{4xy}$的结果为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 0 |
分析 分子利用平方差公式进行因式分解,然后通过约分进行化简.
解答 解:$\frac{{{{({x+y})}^2}-{{({x-y})}^2}}}{4xy}$=$\frac{(x+y+x-y)(x+y-x+y)}{4xy}$=$\frac{4xy}{4xy}$=1.
故选:A.
点评 本题考查了约分.约分时,分子与分母都必须是乘积式,如果是多项式的,必须先分解因式.

练习册系列答案
相关题目
8.我们都知道,先看见闪电后听见雷声,如果光在空气中传播速度为3×108m/s,而声音在空气中的传播速度大约只有300m/s,则光的传播速度是声音传播速度的( )
| A. | 104倍 | B. | 106倍 | C. | 108倍 | D. | 1010倍 |
6.用量角器测得∠MON的度数,下列操作正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
3.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )
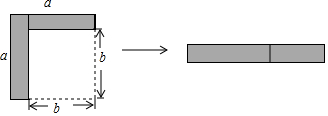

| A. | (a-b)2=a2-2ab+b2 | B. | a(a-b)=a2-ab | C. | (a-b)2=a2-b2 | D. | a2-b2=(a+b)(a-b) |
7.甲,乙两班进行跳绳比赛,参赛学生每分跳绳的个数统计结果如下表:
某同学分析上表后得出如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟跳绳的个数≥150为优秀);
③甲班成绩的波动比乙班大.上述结论中正确的是( )
| 班级 | 参赛人数 | 中位数 | 方差 | 平均字数 |
| 甲 | 55 | 149 | 191 | 135 |
| 乙 | 55 | 151 | 110 | 135 |
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟跳绳的个数≥150为优秀);
③甲班成绩的波动比乙班大.上述结论中正确的是( )
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
8.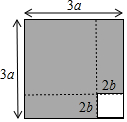 如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
 如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )| A. | 3a+2b | B. | 3a+4b | C. | 6a+2b | D. | 6a+4b |
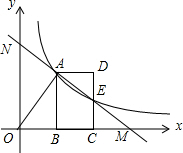 如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.