题目内容
9.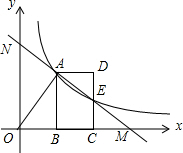 如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.(1)求m的值;
(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数y=$\frac{m}{x}$(x>0)的图象恰好经过DC的中点E,求直线AE的函数表达式;
(3)若直线AE与x轴交于点M,与y轴交于点N,问线段AN与线段ME的大小关系如何?请说明理由.
分析 (1)在Rt△AOB中利用条件可求得A点坐标,利用待定系数法可求得m的值;
(2)可先求得E点纵坐标,代入反比例函数解析式可求得E点坐标,利用待定系数法可求得直线AE解析式;
(3)由直线AE解析式可求得M、N的坐标,利用勾股定理可求得线段AN和ME的长度,比较可求得其大小关系.
解答 解:
(1)∵B(2,0),
∴OB=2,
∵tan∠AOB=$\frac{AB}{OB}$=$\frac{3}{2}$,
∴AB=3,
∴A(2,3),
∵反比例函数y=$\frac{m}{x}$(x>0)的图象经过线段OA的端点A,
∴m=2×3=6;
(2)∵A(2,3),B(2,0),
∴线段AB的中点纵坐标为$\frac{3}{2}$,
∵将线段AB沿x轴正方向平移到线段DC的位置,
∴线段CD的中点E的纵坐标为$\frac{3}{2}$,
由(1)可知反比例函数解析式为y=$\frac{6}{x}$,当y=$\frac{3}{2}$时,可得$\frac{3}{2}$=$\frac{6}{x}$,解得x=4,
∴E(4,$\frac{3}{2}$),
设直线AE解析式为y=kx+b,
把A、E坐标代入可得$\left\{\begin{array}{l}{2k+b=3}\\{4k+b=\frac{3}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{9}{2}}\end{array}\right.$,
∴直线AE的函数表达式为y=-$\frac{3}{4}$x+$\frac{9}{2}$;
(3)相等.理由如下:
在y=-$\frac{3}{4}$x+$\frac{9}{2}$中,令x=0可得y=$\frac{9}{2}$,令y=0可解得x=6,
∴M(6,0),N(0,$\frac{9}{2}$),且A(2,3),E(4,$\frac{3}{2}$),
∴AN=$\sqrt{{2}^{2}+(3-\frac{9}{2})^{2}}$=$\frac{5}{2}$,ME=$\sqrt{(6-4)^{2}+(0-\frac{3}{2})^{2}}$=$\frac{5}{2}$,
∴AN=ME.
点评 本题为反比例函数的综合应用,涉及待定系数法、平移的性质、三角函数的定义、勾股定理等知识.在(1)中利用三角函数的定义求得A点坐标是解题的关键,在(2)中求得E点坐标是解题的关键,在(3)中分别求得M、N的坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.

| A. | 0或3 | B. | 0或-3 | C. | -3 | D. | 3 |
| A. | (a2+2b2)-2(-a2+b2)=3a2+b2 | B. | $\frac{{a}^{2}+1}{a-1}$-a-1=$\frac{2a}{a-1}$ | ||
| C. | (-a)3m÷am=(-1)ma2m | D. | 6x2-5x-1=(2x-1)(3x-1) |
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 0 |
| A. | $\sqrt{(-4)^{2}}$=2 | B. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | C. | ($\sqrt{2}$)2=4 | D. | $\sqrt{6}$÷$\sqrt{2}$=3 |

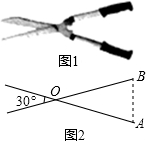 如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A=75度.
如图1是一把园林剪刀,把它抽象为图2,其中OA=OB.若剪刀张开的角为30°,则∠A=75度.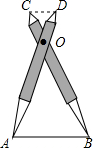 如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )
如图,比例规是一种画图工具,它由长度相等的两脚AD和BC交叉构成,利用它可以把线段按一定的比例伸长或缩短.如果把比例规的两脚合上,使螺丝钉固定在刻度4的地方(即同时使OA=4OD,OB=4OC),然后张开两脚,使A,B两个尖端分别在线段l的两个端点上,若CD=3,则AB的长是( )