题目内容
3.如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )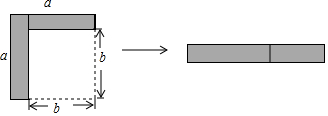
| A. | (a-b)2=a2-2ab+b2 | B. | a(a-b)=a2-ab | C. | (a-b)2=a2-b2 | D. | a2-b2=(a+b)(a-b) |
分析 利用正方形的面积公式和矩形的面积公式分别表示出阴影部分的面积,然后根据面积相等列出等式即可.
解答 解:第一个图形阴影部分的面积是a2-b2,
第二个图形的面积是(a+b)(a-b).
则a2-b2=(a+b)(a-b).
故选D.
点评 本题考查了平方差公式的几何背景,正确用两种方法表示阴影部分的面积是关键.

练习册系列答案
相关题目
13.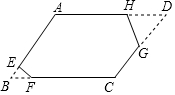 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
 如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
如图,?ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )| A. | 12 | B. | 15 | C. | 16 | D. | 18 |
18.计算$\frac{{{{({x+y})}^2}-{{({x-y})}^2}}}{4xy}$的结果为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 0 |
12.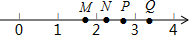 如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )
如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )
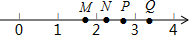 如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )
如图,M,N,P,Q是数轴上的四个点,这四个点钟最适合表示$\sqrt{7}$的是( )| A. | M点 | B. | N点 | C. | P点 | D. | Q点 |
13.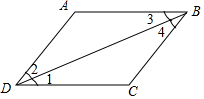 如图,若∠A+∠ABC=180°,则下列结论正确的是( )
如图,若∠A+∠ABC=180°,则下列结论正确的是( )
 如图,若∠A+∠ABC=180°,则下列结论正确的是( )
如图,若∠A+∠ABC=180°,则下列结论正确的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠1=∠3 | D. | ∠2=∠4 |
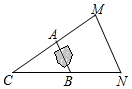 如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.
如图,A,B两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点C,连接CA,CB,分别延长到点M,N,使AM=AC,BN=BC,测得MN=200m,则A,B间的距离为100m.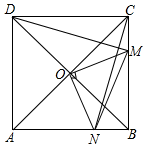 如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是$\frac{1}{2}$,其中正确结论的个数是( )
如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是$\frac{1}{2}$,其中正确结论的个数是( )